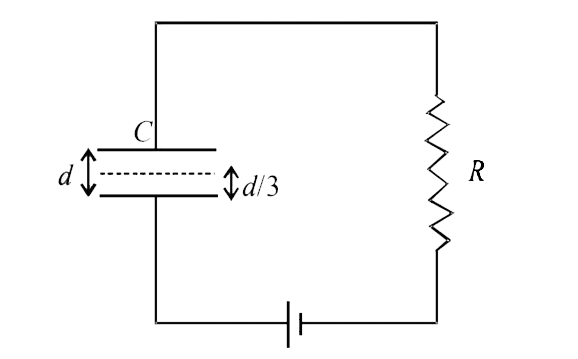
A parallel plate capacitor C with plates of area 1 square unit and separation d is filled with a liquid of dielectric constant K=2. The level of liquid is d/3, initially. If the liquid level decreases at a constant speed v. Then, the capacity of capacitor after t second is

A

$\frac{6 ε_{0}}{5 d + 3 v t}$

B

$\frac{(15 d + 9 v t) ε_{0}}{2 d^{2} - 3 d v t - 9^{2} t^{2}}$

C

$\frac{6 ε_{0}}{5 d - 3 v t}$

D

$\frac{(15 d - 9 v t) ε_{0}}{2 d^{2} + 3 d v t - 9 v^{2} t^{2}}$

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

A parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant $K = 2$ . The level of liquid is $d / 3$ initially. Suppose the liquid level decreases at a constant speed v, the time constant as a function of time t is-

A(a) $\frac{6 e π s l o n_{0} R}{5 d + 3 v t}$
B(b) $\frac{(15 d + 9 v t) ε_{0} R}{2 d^{2} - 3 d v t - 9 v^{2} t^{2}}$
C(c) $\frac{6 ε_{0} R}{5 d - 3 v t}$
D(d) $\frac{(15 d - 9 v t) ε_{0} R}{2 d^{2} - 3 d v t - 9 v^{2} t^{2}}$
A parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant $K = 2$ . The level of liquid is $d / 3$ initially. Suppose the liquid level decreases at a constant speed v, the time constant as a function of time t is-

A $\frac{6 ε_{0} R}{5 d + 3 / t}$
B $\frac{(15 d + 9 v t) ε_{0} R}{2 d^{3} - 3 d v t - g v^{2} t^{2}}$
C $\frac{6 ε_{0} R}{5 d - 3 v t}$
D $\frac{(15 d - 9 v t) ε_{0} R}{2 d^{3} + 3 d v t - 9 v^{2} t^{2}}$
A parallel plate capacitor of area ‘A’ plate separation ‘d’ is filled with two dielectrics as shown. What is the capacitance of the arrangement ?

A $\frac{3 K ε_{0} A}{4 d}$
B $\frac{4 K ε_{0} A}{3 d}$
C $\frac{(K + 1) ε_{0} A}{2 d}$
D $\frac{K (K + 3) ε_{0} A}{2 (K + 1) d}$

AAKASH SERIES-CAPACITORS -PRACTICE SHEET (ADVANCED) (Straight Objective Type Questions)

Home
Ask Doubt
Profile