A long round conductor of cross-sectional area S is made of material whose resistivity depends only on a distance r from the axis of the conductor as ρ=α/r2, where α is a constant. Find the total resistance per unit length of the rod when potential difference is applied across its length.
παS2
2παS2
πα2S2
αS2
The correct Answer is:B
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) (Integer Type Questions))
5 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II PRACTICE SHEET (ADVANCED) (Straight Objective Type Questions))
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -I(MAIN) (Straight Objective Type Questions))
6 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
44 Videos
Similar Questions
A long round conductor to cross-sectional area S is made of material whose resistivity depends only on a distance r from the axis of the conductor as ρ=α/r4, where α is a constant. Find :
(a) the resistance per unit length of such a conductor,
(b) the electric field strength in the conductor due to which a current I flow though it.
View SolutionA long cylindrical conductor of cross-sectional area A and radius a is made of material whose resistivity depends only on a distance r from the axis of conductor, given by ρ=cr2, where c is a constant. Find the resistance per unit length of the conductor and the electric field strength due to which a current I flows in it.
View Solution
Knowledge Check
A solid cylinder of length l and cross-sectional area A is made of a material whose resistivity depends on the distance r from the axis of the cylinder as ρ=k/r2 where k is constant . The resistance of the cylinder is -
AπklA2B2πklA2CπklADNoneA conductor of length l and area of cross-section A has a resistance R then its specific resistance is
Aρ=RAlBρ=RAlCρ=lRADρ=R2AlA solid cylindrical wire of length l has cross-section radius a as shown below. The specific resistance of material is given as ρ=ρ0r, where r is distance from axis of cylinder and ρ0 is a positive constant quantity. The resistance across its ends is :
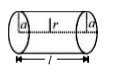 Aρ0l2πaBρ0lπa2Cρ0lπaD2ρ0lπ
Aρ0l2πaBρ0lπa2Cρ0lπaD2ρ0lπ
A conductor of uniform area of cross section A has a variable resistivity along its length. What will be the resistance of the conductor if ρ=ρ0(1+αx2), at length l.
View SolutionAnswer questio numbers (a)-(d) on the basis of your understanding of the following paragraph and the related studied concepts:
We know that current flowing through a conductor depends upon its resistance and potential difference across its ends. The resistance of the conductor depends of (i) its length (ii) its area of cross section and (iii)on the nature of its material. PRecise measurements show that resistance of a uniform metallic conductor is directly proportional to its length (l) and inversely proportional to the area of cross section (A). thus, we can write
R=ρlA where p is a constant whose value depends on the material of the conductor.
WHo studied the relation between current flowing through a conductor and potential difference across its ends?
(b) State the relationship between current, resistance and potential difference in a mathematical form.
(c) Name the constant p whose value depends on the material of the conductor and give its SI unit.
(d) How does value of p governs your choice of material to be used as live wire for electrical fittings in your house? Name two suitable materials.
View SolutionResistivity of the material of a conductor of uniform cross-section varies along its length as ρ=ρ0(1+αx). Find its resistance if its length is L and area of cross-section is A.
View SolutionA rod of length L with sides fully insulated is made of a material whose thermal conductivity K varies with temperature as K=αT where α is constant. The ends of rod are at temperature T1 and T2(T2>T1) Find the rate of heat flow per unit area of rod .
View SolutionA long round dielectric cyclinder is polarized so that teh vector P=αr, where α is a positive constant and r is the distance from the axis. Find the space density ρ' of bound chagres as a function of distance r from the axis.
View Solution
