The resistivity of cylindrical conductor carrying steady current along its length varies linearly with the distance from the current carrying end as given by ρ=ρ0(1+xl) where l is the length of the conductor and x is the distance from the current entry and. ρo is a positive constant.
Electric field varies linearly with x
Electric potential difference across the length varies linearly with x
Volume charge density in the conductor is zero
volume charge density in the conductor is non zero.
The correct Answer is:A, B
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS
94 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA
101 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II PRACTICE SHEET (ADVANCED) (Straight Objective Type Questions))
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
44 Videos
Similar Questions
Knowledge Check
Variation of magnetic field with distance from current carrying conductor is:
AB∝a2BB∝1a2CB∝aDB∝1aA straight horizontal conductor carries a steady electric current from south to north
Athe needle remains perpendicular to the conductorBthe needle remains parallel to the conductorCthe north pole of the needle is deflected towards eastDthe north pole of the needle is deflected towards westA cylindrical conductor of radius R is carrying constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor , is correctly represented by the figure:
A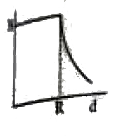 B
B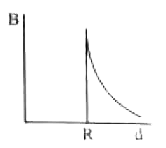 C
C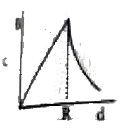 D
D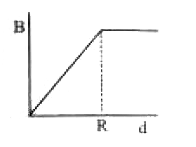
The linear mass density i.e. mass per unit length of a rod of length L is given by ρ=ρ0(1+xL), where ρ0 is constant , x distance from the left end. Find the total mass of rod and locate c.m. from the left end.

View SolutionThe density of a rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.

View SolutionA conductor of uniform area of cross section A has a variable resistivity along its length. What will be the resistance of the conductor if ρ=ρ0(1+αx2), at length l.
View SolutionThe density of a linear rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.

View SolutionA cylindrical conductor of radius R is carrying a constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor, is correctly represented by the figure
View Solution
