एक फलन f समुच्चय X से Y तक आच्छादक है। यदि प्रत्येक yεY के लिए xεX का अस्तित्व इस प्रकार है कि f(x)=y यदि नहीं हो तो इसके विपरीत लिया जाता है यदि एक वास्तविक फलन आच्छादक होगा यदि यह सभी वास्तविक मानों को लेता है अन्यथा एक अंतः क्षेपी फलन होगा अतः यदि X तथा Y सीमित समुच्चय है तो f आच्छादक नहीं हो सकता यदि Y,X से अधिक अवयवों को लेता है।
बहुपद फलन a0xn+a1xn−1+…………+an=0,a0≠0 आच्छादक है यदि
सभी धनात्मक पूर्णांकों n के लिए
सभी सम धनात्मक पूर्णांकों n के लिए
सभी विषम धनात्मक पूर्णांको n के लिए
धनात्मक पूर्णांक नहीं है
The correct Answer is:C, D
Step by step video, text & image solution for एक फलन f समुच्चय X से Y तक आच्छादक है। यदि प्रत्येक y epsilon Y के लिए x epsilon X का अस्तित्व इस प्रकार है कि f(x)=y यदि नहीं हो तो इसके विपरीत लिया जाता है यदि एक वास्तविक फलन आच्छादक होगा यदि यह सभी वास्तविक मानों को लेता है अन्यथा एक अंतः क्षेपी फलन होगा अतः यदि X तथा Y सीमित समुच्चय है तो f आच्छादक नहीं हो सकता यदि Y,X से अधिक अवयवों को लेता है। बहुपद फलन a_(0)x^(n)+a_(1)x^(n-1)+…………+a_(n)=0,a_(0)!=0 आच्छादक है यदि by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - फलन, सीमा, सांतत्य तथा अवकलनीयताEXERCISE - JEE ADVANCED( MATCH THE COLUMN TYPE)13videos
फलन, सीमा, सांतत्य तथा अवकलनीयता
- BOOK - ERRORLESS HINDICHAPTER - फलन, सीमा, सांतत्य तथा अवकलनीयताEXERCISE - JEE ADVANCED( PASSAGE TYPE)9videos
फलन, सीमा, सांतत्य तथा अवकलनीयता
- BOOK - ERRORLESS HINDICHAPTER - प्रायिकताEXERCISE - EXERCISE99videos
प्रायिकता
- BOOK - ERRORLESS HINDICHAPTER - लघुगणक और आंशिक भिन्नें EXERCISE - JEE Advanced (integer type questions)8videos
लघुगणक और आंशिक भिन्नें
Similar Questions
कॉलम I में दिए गए वक्तव्यों/व्यंजकों का कॉलम II में दिये गये मानों से सुमेल करे।
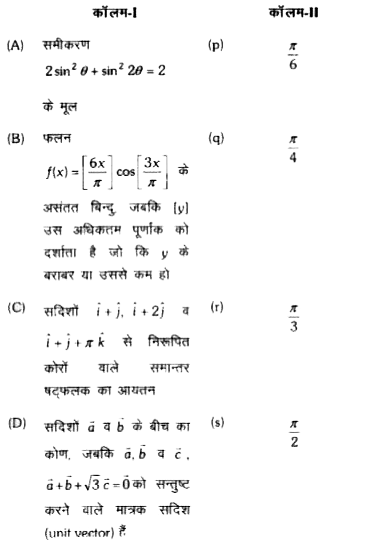 01:29View Solution
01:29View Solutionकथन-1 प्रत्येक फलन, एक सम फलन तथा एक विषम फलन के योग के रूप में अद्वितीय परिभाषित किया जा सकता है।
कथन-2 प्राचल a के मानों का समुच्चय [9,∞) है जिसके लिए फलन f(x) को f(x)=tan(sinx)+[x2a] के द्वारा समुच्चय [−3,3] में एक विषम फलन परिभाषित किया जाता है।00:53View SolutionA, B, C तीन परस्पर स्वतंत्र घटनायें हैं। S1 तथा S2 दो कथनों को देखने पर
S1 : A तथा B∪C स्वतन्त्र हैं
S2 : A तथा B∩C स्वतन्त्र हैं तब02:06View Solutionपद 6+log32⎛⎜ ⎜⎝13√2 ⎷4−13√2 ⎷4−13√2√4−13√2…⎞⎟ ⎟⎠ का मान है
04:19View Solutionदिखाइए कि, फलन f(x)={xयदि x एक पूर्णांक है|0यदि x एक पूर्णांक नहीं है|, x के प्रत्येक मान के लिए असतत है |
04:40View Solutionयदि फलन f(x) द्वारा अधिकतम मान x व y न्यूनतम मान ग्रहण किया जाता है तो इस फलन का आयाम . . . . . . . है ।
05:40View Solutionयदि द्विअवकलनीय f(x) फलन x=a पर स्थानीय उच्चिष्ठ है , तो
04:51View Solutionयदि f(x)=8−xPx−4 , तो फलन का परिसर क्या होगा?
03:20View Solutionफलन y=f(x) के लिए यदि dydx=6(x−2)(x−3) है तो के ty अधिकतम मान के लिए का x मान ज्ञात कीजिये
01:27View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
04:50View Solutionयदि f(x)=xयदिx परिमेय है 0यदिx अपरिमेय है तथा g(x)=0यदिx परिमेय हैx यदिx अपरिमेय है तबf−g है
04:24View Solutionनिम्न में से कौन-सा फलन वास्तविक संख्याओं के समुच्चय में एकैकी आच्छादक है?
04:11View Solutionयदि फलन f (x) आवर्त का सतत फलन है , तो समाकलन I=∫a+Taf(x)dx का मान है
02:47View Solutionएक फलन g जो प्रत्येक वास्तविक संख्या x>0 के लिए परिभाषित है तथा g(1)=1,g'(x2)=x3 को सभी x>0 के लिए सन्तुष्ट करता है, तो g (4) का मान है
03:18View Solutionयदि m,n∈R तथा f:R→R एक सतत फलन है जो
f(x)={m2cos2x+n2sin2x, यदि x≤0 emx+n, यदि x>0
द्वारा दिया जाता है, जब02:43View Solutionयदि वास्तविक चर का वास्तविक मान फलन । इस प्रकार है कि 1(1+x)(1+x2)=A1+x+f(x)1+x2 है तो f (x) किसके बराबर है?
02:44View Solution

