माना कि फलन
f1:R→R,f2:(−π2,π2)→R,f3:(−1,eπ2−2)→R और f4:R→R इस प्रकार परिभाषित है कि
(i) f1(x)=sin(√1−e−x2),
(ii) f2(x)={|sinx|tan−1xifx≠01ifx=0 जहां प्रतिलोम त्रिकोणमितीय फलन tan−1x,(−π2,π2) में मान धारण करता है
(iii) f3(x)=[sin(loge(x+2))], जहां tεR के लिए [t],t से छोटा या t के बराबर महत्तम पूर्णांक को दर्शाता है।
(iv) f4(x)=⎧⎨⎩x2sin(1x)यदिx≠0xयदिx=0

The correct Answer is:A, B, C, D
Step by step video, text & image solution for माना कि फलन f_(1):RtoR,f_(2):(-(pi)/2,(pi)/2)to R,f_(3):(-1,e^((pi)/2)-2)toR और f_(4):RtoR इस प्रकार परिभाषित है कि (i) f_(1)(x)=sin(sqrt(1-e^(-x^(2)))), (ii) f_(2)(x)={((|sinx|)/(tan^(-1)x)"if",x!=0),(1,"if"x=0):} जहां प्रतिलोम त्रिकोणमितीय फलन tan^(-1)x,(-(pi)/2,(pi)/2) में मान धारण करता है (iii) f_(3)(x)=[sin(log_(e)(x+2))], जहां t epsilon R के लिए [t],t से छोटा या t के बराबर महत्तम पूर्णांक को दर्शाता है। (iv) f_(4)(x)={(x^(2)sin(1/x),यदि x!=0),(x,यदिx=0):} by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - फलन, सीमा, सांतत्य तथा अवकलनीयताEXERCISE - JEE ADVANCED( INTEGER TYPE)40videos
फलन, सीमा, सांतत्य तथा अवकलनीयता
- BOOK - ERRORLESS HINDICHAPTER - प्रायिकताEXERCISE - EXERCISE99videos
प्रायिकता
- BOOK - ERRORLESS HINDICHAPTER - लघुगणक और आंशिक भिन्नें EXERCISE - JEE Advanced (integer type questions)8videos
लघुगणक और आंशिक भिन्नें
Similar Questions
माना एक फलन जो संबंध
f(2tanx1+tan2x)=(1+cos2x)(sec2x+2tanx)2 को संतुष्ट करता है।
कथन-1 y=f(x) का परिसर R है।
कथन-2: रेखीय फलन का परिसर R होगा यदि प्रांत R है।05:42View SolutionA, B, C तीन परस्पर स्वतंत्र घटनायें हैं। S1 तथा S2 दो कथनों को देखने पर
S1 : A तथा B∪C स्वतन्त्र हैं
S2 : A तथा B∩C स्वतन्त्र हैं तब02:29View Solutionपद 6+log32⎛⎜ ⎜⎝13√2 ⎷4−13√2 ⎷4−13√2√4−13√2…⎞⎟ ⎟⎠ का मान है
02:22View SolutionFor x varepsilon R,x!=0,x!=1, Let f_(0)(x)=(1)/(1-x) and f_(n+1)(x)=f_(0)(f_(n)(x)),n=0,1,2,3...... Then the value of f_(100)(3)+f_(1)((2)/(3))+f_(2)((3)/(2)) is equal to:
04:39View SolutionIf f_(1)(x)=2x,f_(2)(x)=3sin x-x cos x then for x in(0,(pi)/(2))
05:04View SolutionLet f(1):R→R,f2:[0,∞)→R,f3:R→Randf4:R→[0,∞) be a defined by
f1(x)={|x|if x<0exif x>0:f2(x)=x2,f3(x)={sinxif x<0xif x≥0 and f4(x)={f2(f1(x))if x<0f2(f1(f1(x)))−1if x≥0 Then, f4 is04:37View SolutionLet f1(x)andf2(x) be twice differentiable functions where F(x)=f1(x)+f2(x)andG(x)=f1(x)−f2(x),∀x∈R,f1(0)=2andf2(0)=1.Iff'1(x)=f2(x)andf'2(x)=f1(x),∀x∈R. then the number of solutions of the equation (F(x))2=9x4G(x)is...... .
11:44View SolutionLet f1:R→R,f2:[0,∞)→R,f3:R→R be three function defined as
f1(x)={|x|x<0exx≥0,f2(x)=x2,f3(x)={f2(f1(x))x<0f2(f1(x))−1x≥0 then f3(x) is:04:21View SolutionIf f1(x)=2x,f2x(=3sinx−xcosx, for x∈(0,π2)
View Solutionमाना कि फलन
f1:R→R,f2:(−π2,π2)→R,f3:(−1,eπ2−2)→R और f4:R→R इस प्रकार परिभाषित है कि
(i) f1(x)=sin(√1−e−x2),
(ii) f2(x)={|sinx|tan−1xifx≠01ifx=0 जहां प्रतिलोम त्रिकोणमितीय फलन tan−1x,(−π2,π2) में मान धारण करता है
(iii) f3(x)=[sin(loge(x+2))], जहां tεR के लिए [t],t से छोटा या t के बराबर महत्तम पूर्णांक को दर्शाता है।
(iv) f4(x)=⎧⎨⎩x2sin(1x)यदिx≠0xयदिx=0
 07:47View Solution
07:47View Solutionf: R→R; f(x)=xsinx+cosx+sin2x .If f(x)=f1(x)+f2(x) where f1,f2 are odd and even. function respectively with the same domain as f ,then (f1−f2)(π2)=
1) π2
2) −π2
3) 0
4) π07:47View SolutionLet [x] = greatest integer ≤x and {x}=x−[x],
Let, f1(x)=2π[sin−1(x)+cos−1(x)]
f2(x)=sin2(log5x)+cos2(log3x)
f3(x)=sgn({x}+1)
and f4(x)=sec2[{x}]−tan2{[x]}
sgn(x)=⎧⎪⎨⎪⎩−1ifx<00ifx=01if>0
Then which of the follwing is not true?05:28View SolutionSupposed that f_(1):RtoR,f_(2):[0,oo)toR,f_(3):RtoR And f_(4):rto[0,oo) As follows f_(1)(x)={((|x),यदि,xlt0),(e^(x),यदि,xge0):} f_(2)(x)=x^(2) f_(3)(x)={(sinx, यदि,xlt0),(x, यदि,xge0):} And f_(a)(x)={(f_(2)(f_(1)(x)),यदि,xlt0),(f_(2)(f_(1)(x))-1,यदि ,xge0):}
06:07View Solutionमाना की f1:R→R2,f2:[0,∞)→R,f3:R→R और f4:R→[0,∞) निम्नानुसार
f1(x)={|x| यदि x<0ex यदि x≥0
f3x={sinx यदि x<0x यदि x≥0
f4(x)={f2(f1(x)) यदि x<0f2(f1(x))−1 यदि x≥0 परिभाषित है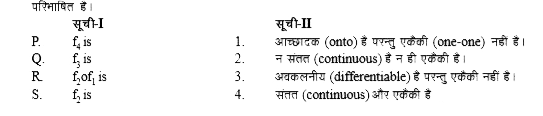 05:58View Solution
05:58View SolutionFor x∈R,x≠0,x≠1, let f0(x)=11−x and fn+1(x)=f0(fn(x)),n=0,1,2,.... Then the value of f100(3)+f1(23)+f2(32) is equal to
06:44View Solution

