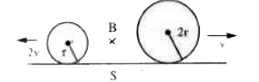
Two conducting rings of radii r and 2r move in opposite directions with velocities 2v and v respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicular to the plane of the rings. The potential difference between the highest points of the two rings is
Replace the induced emfs in the rings by cells of emfs
e1=B2r(2v)=4Brv,e2=B(4r)=4Brv
The equivalent circuit is
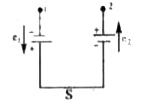
Hence the potential difference between the highest points of the two rings is V2−V1=e1+e2=8Brv
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IA
33 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IB
18 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
32 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
20 Videos
Similar Questions
Two conducting rings P and Q of radius r and 3r move in opposite directions with velocities 2v and v respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicular to the plane of the rings. The potential difference between the highest points of the two rings a
View SolutionTwo conducting rings of radii r and 2r move in apposite directions with velocities 2υ and υ respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicular to the plane of the rings. The potential difference between the highest points of the two rings is
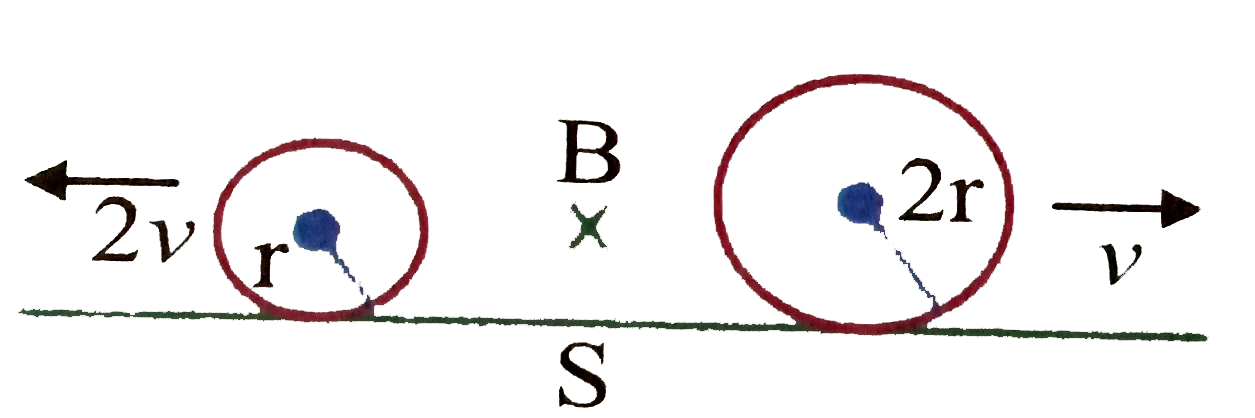
View Solution
Knowledge Check
Two conducting rings P and Q of radius r and 3r move in opposite directions with velocities 2v and v respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicular to the plane of the rings. The potential difference between the highest points of the two rings a
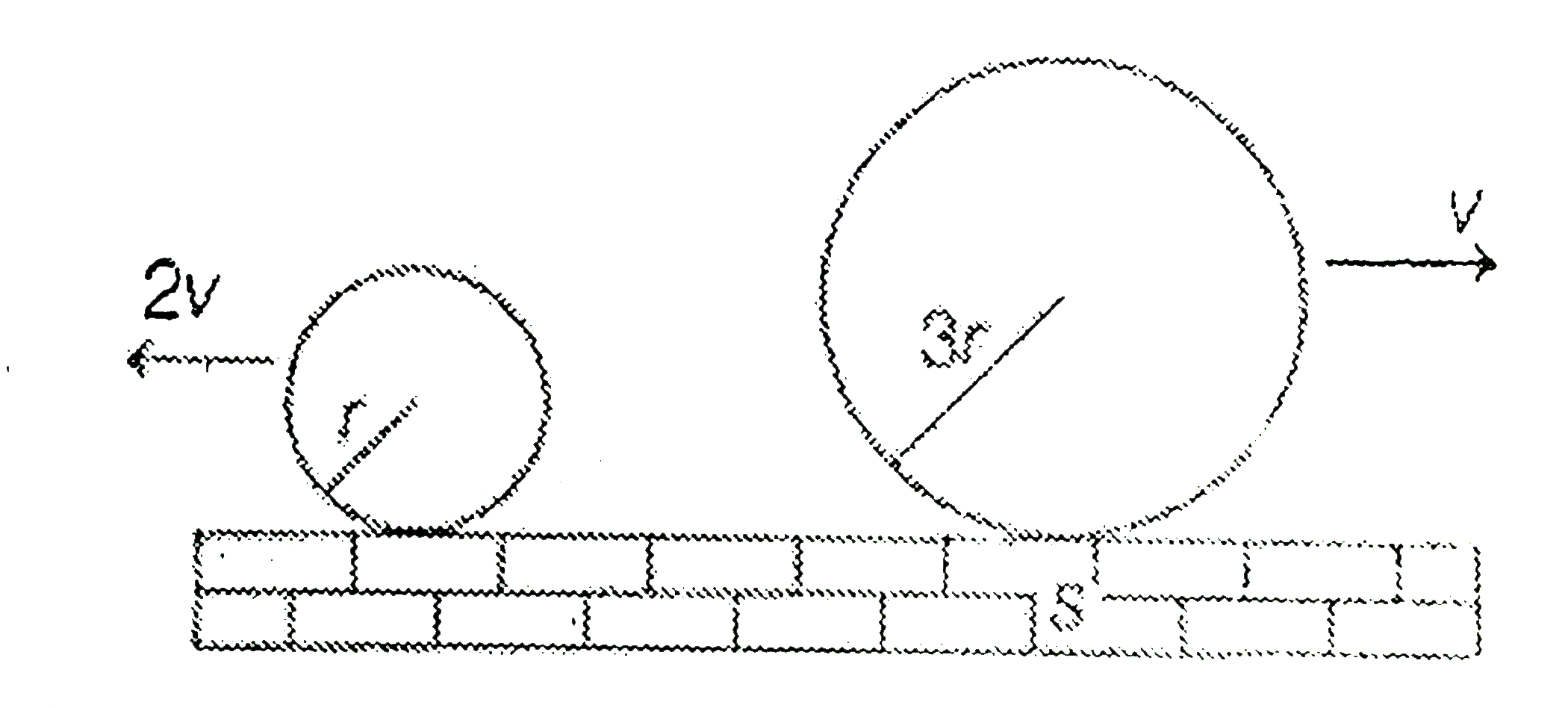 AzeroB2BrvC6BrvD10Brv
AzeroB2BrvC6BrvD10BrvTwo identical conducting rings A and B of radius R are rolling over a horizontal conducting plane with same speed v but in opposite direction. A constant magnetic field B is present pointing into the plane of paper. Then the potential difference between the highest points of the two rings is
 A0B2BvRC4BvRDnone of these
A0B2BvRC4BvRDnone of theseA conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.
Two conducting rings of radii r and 2r move in apposite directions with velocities 2υ and υ respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicular to the plane of the rings. The potential difference between the highest points of the two rings is
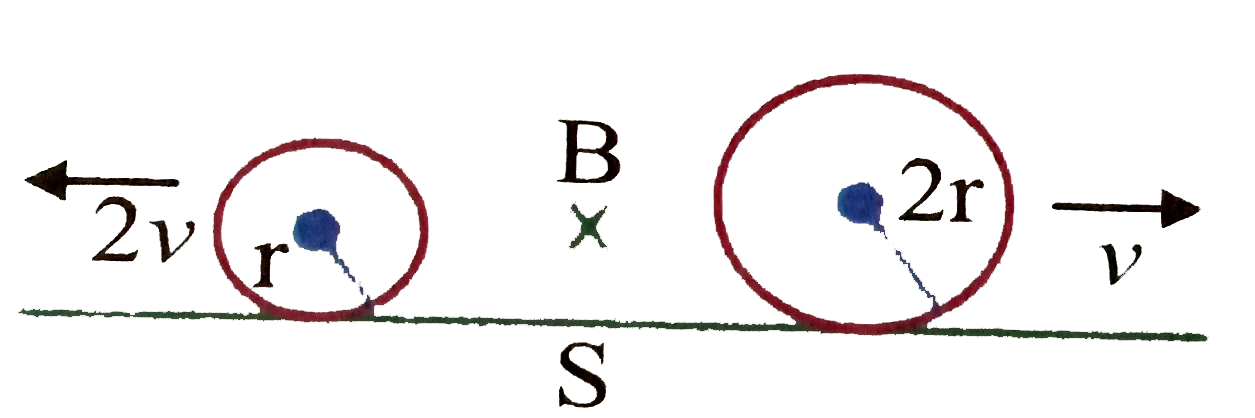
View SolutionTwo rings of radii 5m and 10m move in opposite directions with velocity 20 m/s and 10 m/s respectively, on a conducting curface S. There is a uniform magnetic field of magnitude 0.1T perpendicular to the plane of the rings. Find the potential difference between the highest points of the two rings.
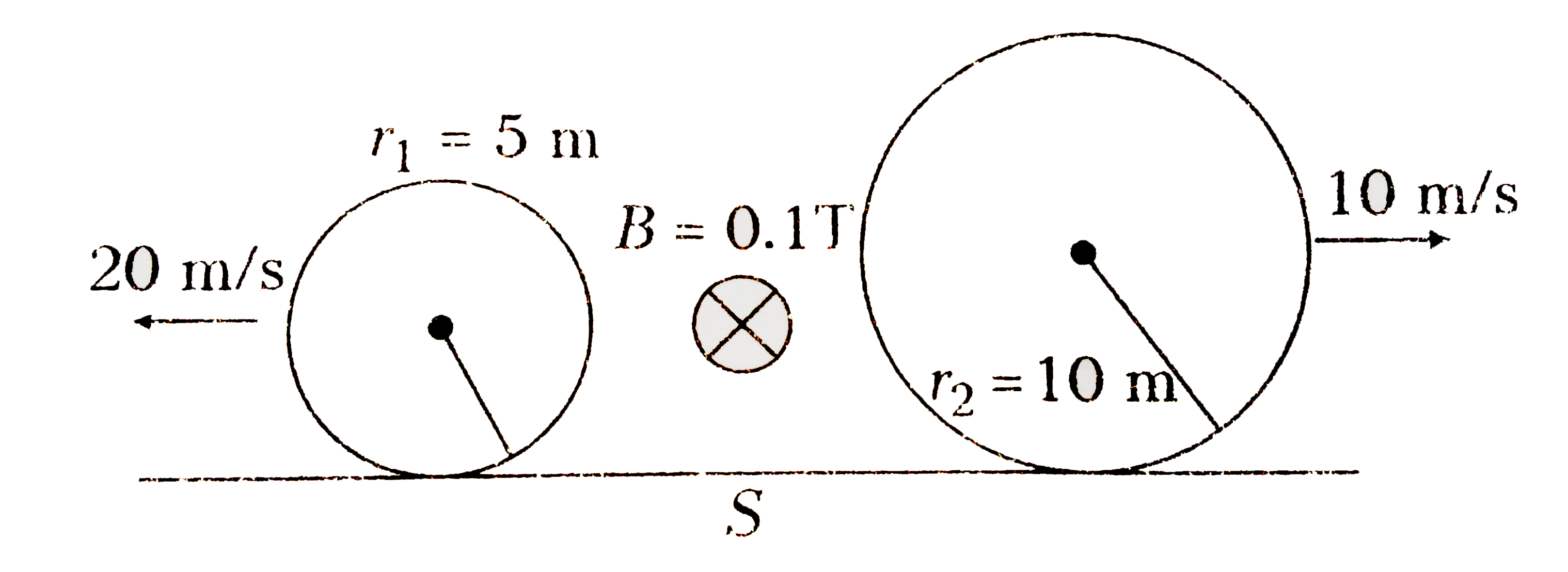
View SolutionTwo rings of radii 5m and 10m move in opposite directions with velocity 20 m/s and 10 m/s respectively, on a conducting curface S. There is a uniform magnetic field of magnitude 0.1T perpendicular to the plane of the rings. Find the potential difference between the highest points of the two rings.
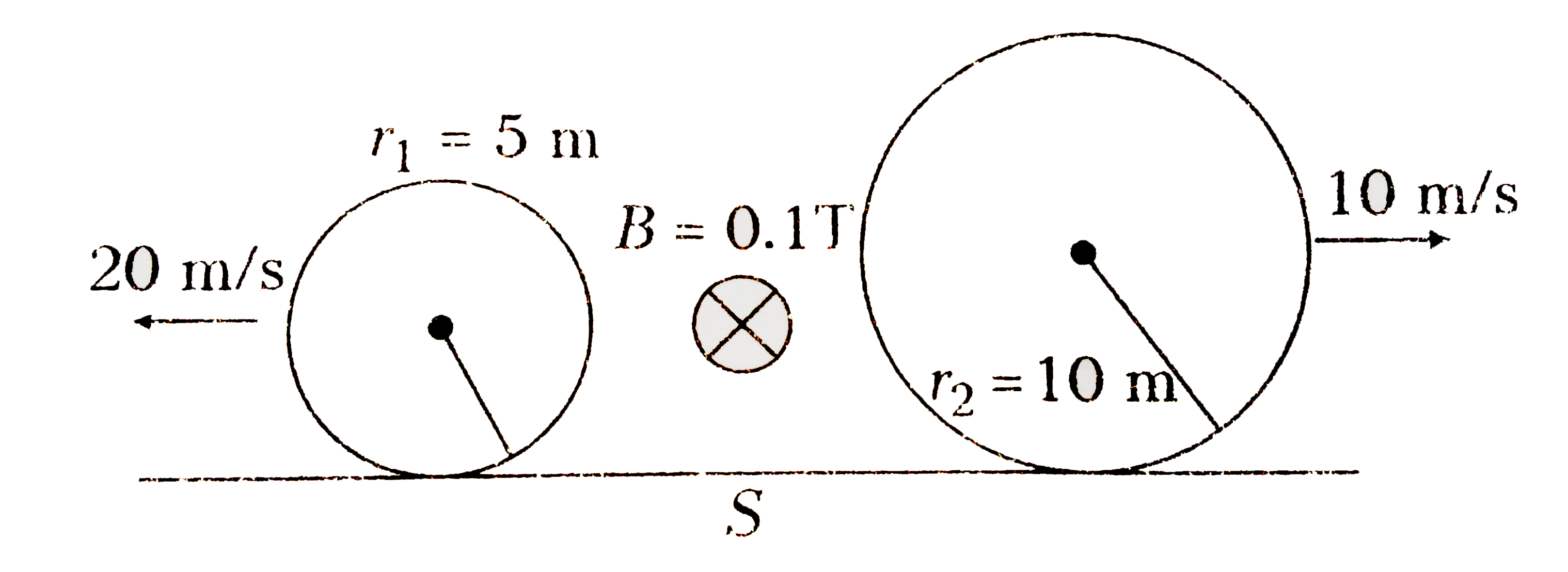
View SolutionTwo identical conducting rings A and B of radius R are rolling over a horizontal conducting plane with same speed v but in opposite direction. A constant magnetic field B is present pointing into the plane of paper. Then the potential difference between the highest points of the two rings is

View SolutionTwo identical conducting rings A and B of radius R are rolling over a horizontal conducting plane with same speed v but in opposite direction. A constant magnetic field B is present pointing into the plane of paper. Then the potential difference between the highest points of the two rings is

View Solution
