Relation between linear and angular velocity for object in rotational motion is $\to v = \to r \times \to ω$ Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

The relation between the linear speed and angular speed of particle of rotation motion is $v = r ω$ , where r is the radius of circular path.
In general by any instant
$v_{i} = r_{i} ω$ where $i = 1, 2, 3, \dots ., n$ and n is the no. of particles in the rigid body.
If $r = 0, v = 0$ , means particles on axis are stationary.

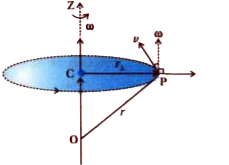
For obtaining the relation between linear velocity and angular velocity, a particle P of a rigid body rotating about Z-axis (fixed) as shown in figure. The position vector $- - \to O P = \to r$ of particle at P on the rigid body with respect to the origin O. Its perpendicular distance is $r_{1}$ from the centre C circular path.
Now $\to ω \times \to r = \to ω \times - - \to O P$
$= \to ω \times (- - \to O C + - - \to C P)$
$= \to ω \times - - \to O C + \to ω \times - - \to C P$
but $\to ω \times - - \to O C = ω (O C) {sin 0}^{\circ}$
[ $∵ \to ω and - - \to O C$ are in same direction]
= 0
$∴ \to ω \times \to r = \to ω \times - - \to C P$
but $\to ω$ perpendicular to the radius $- - \to C P$ and is parallel to the tangent of circle at P.
$∴ \to ω \times \to r = \to ω \times - \to r_{⊥} [∵ - - \to C P = - \to r_{⊥}]$
$= ω r_{⊥} {sin 90}^{\circ}$
[ $∵ \to ω and - \to r_{⊥}$ are perpendicular]
$= ω r_{⊥}$
but $= ω r_{⊥}$ is equal to the magnitude linear velocity at point P
$∴ \to ω \times \to r = \to v$
Is the relation between angular velocity and linear velocity.
The direction of $\to ω$ does not change with time for a rotating body about a fixed time but its magnitude change with time.
It the axis is not remain fixed, direction of angular velocity changes with time.
Hence, in general, for a rotating body the magnitude and direction of $\to ω$ changes with time.

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-SECTION-F (SECTION-D) QUESTIONS PAPER

Home
Ask Doubt
Profile