Question

Obtain mirror equation for the real image obtained by concave mirror.

Explanation

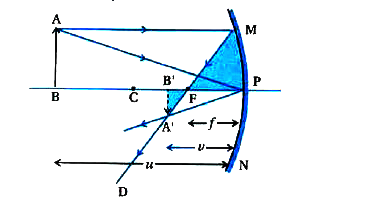
An object AB is perpendicular to principal axis away from C of a concave mirror.
AM ray from point A incidents on mirror at M and reflected ray passes through principal focus F.
AP ray from point A incidents on pole P and reflects back in form of PA.
These both reflected rays intersect at A., hence A. is real image of A.
A.B. is image of object AB due to reflection of rays from mirror.
Let FP = focal length f
CP = radius of curvature R
BP = object distance u
B.P= image distance v
For paraxial rays, MP can be considered to be a straight line perpendicular to CP.
The two right-angled triangles A.B.F and MPF are similar.
`therefore(B.A.)/(PM)=(B.F)/(FP)`
But PM = BA
`therefore (B.A.)/(BA)=(B.F)/(FP)`....(1)
Since `angleAPB = angleA.PB.`, the right angled triangles A.B.P and ABP are also similar. Therefore,
`therefore(B.A.)/(BA)=(B.P)/(BP)` ...(2)
Comparing Equations (1) and (2),
`(B.F)/(FP)=(B.P)/(BP)`
but B.F = B.P - FP
`therefore (B.P-FP)/(FP)=(B.P)/(BP)` ....(3)
Now, according to sign convention, B.P = - v, FP = - f, BP = - u
From equation (3),
`(-v+f)/(-f)=(-v)/(-u)`
`therefore (v-f)/(f)=v/u`
`therefore v/f-1=v/u`
`therefore v/f=1+v/u`
Now,dividing by v,
`therefore 1/f=1/v+1/u`
Which is mirror equation and it is called Gaussian equation as it was given by scientist Gauss.