Question

Explain the minimum deviation angle for prism by graph of deviation angle versus incidence angle.

Explanation

The graph of experimentally measured values of the angle of deviation against the values of angle of incidence i is shown in the figure.

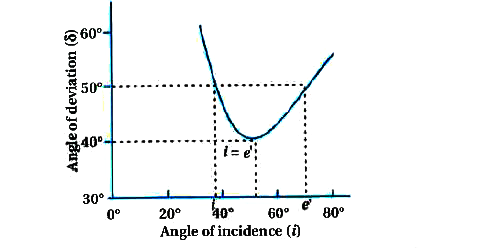
From the graph it is clear that the value of the angle of deviation becomes minimum for only one particular value of the angle of incidence i.
Also we can see that for two values of angle of incidence angle of deviation is same.
It has been experimentally established that for any given prism the ray for which the angle of incidence and angle of emergence are equal the angle of deviation is minimum for that ray.
This angle is called the angle of minium deviation of the given prism for the incident monochromatic light.
Note that,
when `i=e implies delta=delta_m`
For prism
`i+e=A+delta` ...(1)
the condition for minimum deviation angle.
i=e then `delta=delta_m`
`thereforei+i=A+delta_m`
`therefore2i =A=delta_m`
`therefore i=(A+delta_m)/(2)` ...(2)
According to Snell.s Law for AB surface,
`n_1sin i=n_2sin r_1` ... (3)

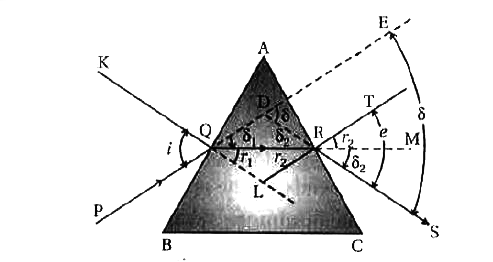
From equation (3) & (4)
`n_1sine=n_2sinr_2` ... (4) (i=e)
`therefore` sin i =sin e
`therefore n_2sinr_1=n_2sinr_2`
`r_1=r_2=r` (Suppose)
`r_1+r_2=A`
r+r=A
`r=A/2` ... (5)
Using this result in equations (3) and (4)
`n_1sin i =n_2sin r`
`n_1sin i =n_2sinA/2` ... (6)
[`because` From eqn.(5)]
Using this result in equation (6)
`n_1sin((A+delta_m)/(2))=n_2sinA/2`
`(sin((A+delta_m)/(2)))/(sin(A/2))=(n_2)/(n_1)`
If prism is kept in air then, `n_1`, = 1 and `n_2` = 1 So, above equation is,
`n=(sin((A+delta_m)/(2)))/(sin(A/2))`
This equation shows that for a given prism value of `delta_m` depends on the angle of prism and th refractive index of the material of prism and th medium in which the prism is kept.
Remember : When `delta` is minium ray QR passin through the prism travels parallel to the base B of the prism.