Question

A vessel is fully filled with liquid having refreactive index $\frac{5}{3}$ . At the bottom of the vessel a point-like source of light is kept. An observer looks at the source of light from the top. Now, an opaque circular disc is kept on the surface of the water in such a way that its centre just rests above the light source. Now liquid is taken out from the bottom gradually. Calculate the maximum height ofthe liquid to be kept so that light source cannot be seen from outside. (Radius of the disc is 1 cm.)

Explanation

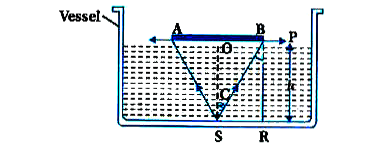
`rArr n = 5/3 OA = OB = r= 1 cm`
`rArr` At the bottom of vessel S is source opaque disc AB is on water surface ray of light coming out of S are `vec SB and vec SA`.
Water surface goes down as water comes out bottom of vessel slowly so disc goes down ar `angle SBR` increases.
`rArr` When `angleSBR` = critical angle C ray goes in direction of BP and experiences total internal reflection.
`therefore` Taking `angleSBR` = C in `Delta` SOB,
We can solve it in two ways.
Method : 1
`tan C = (OB)/(OS) therefore tan C = (1 cm )/(h) ....... (1)`
but , `sin C = 1/n = 3/5`
`therefore cos C = sqrt(1 - sin^2C)= sqrt((1-9)/(25)) = sqrt(16/25)`
`therefore cos C = 4/5`
`therefore tan C = (sin C )/(cos C) = 3/4`
`therefore (1)/(h) = (3)/(4)` [From (1)]
`therefore h = 4/3 = 1.33 cm = 133 mm `
Method : 2
`sin C = 1/n`
`therefore sin C = 3/5 = 0.6`
`therefore C = 36^@ 54.`
From figure , `tan C = r/h`
`therefore h = (r)/(tan 36^@54) therefore h = (1)/(0.7508) = (1)/(0.75) = 4/5`
`therefore h = 1.33 cm = 1.33 mm`