A tank is filled with two immiscible liquids of densities 2ρandρ each of height h. Two holes are made to the side wall at h2and3h2 from upper surface of the liquid, then find the ratio of velocity of efflux of the liquids through the holes
According to Bernoullis theorem, to find v1

P+ρg(h2)=P+12(ρ)(v21)⇒v1=√gh
to find v2,P+(ρgh)+(2ρ)g(h2)=12(2ρ)v22+P
⇒v2=√2gh∴v1v2=1√2
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDS BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-IA
175 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-IB (ASSERTION & REASON)
46 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
108 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE - 3
26 Videos
Similar Questions
Equal volumes of two immiscible liquids of densities ρ and 3ρ are filled in a big vessel. Two small holes are punched at depth h/3 and 4h/3 from upper surface of lighter liquid. If v1 and v2 are velocities of efflux at these two holes, then v1/v2 is

View SolutionEqual volumes of two immiscible liquids of densities ρ and 3ρ are filled in a big vessel. Two small holes are punched at depth h/3 and 4h/3 from upper surface of lighter liquid. If v1 and v2 are velocities of efflux at these two holes, then v1/v2 is

View Solution
Knowledge Check
Equal volume of two immissible liquid of densities ρ and 2ρ are filled in a vessel as shown in Fig. 7(CF).15. Two small holes are punched at depth h2 and 3h2 from the surface of lighter liquid. If v1 and v2 are the velocities of efflux at these two holes, then v1/v2 is
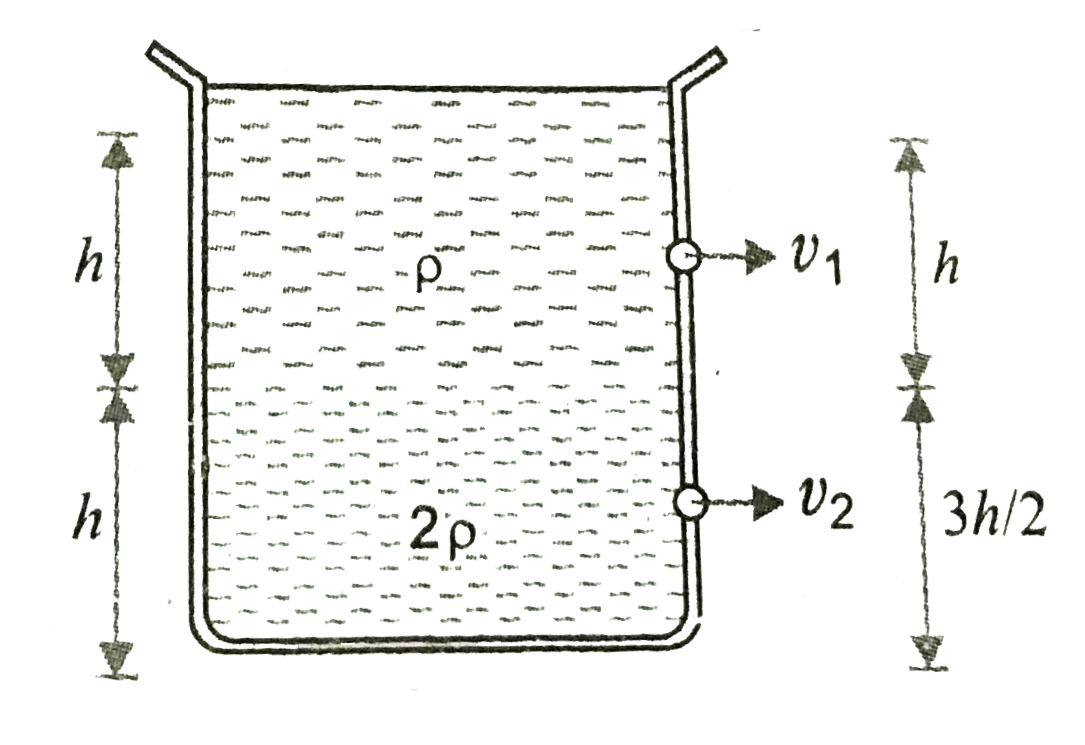 A14B12C1√2D12√2
A14B12C1√2D12√2Equal volume of two immiscible liquids of densities ρ and 2ρ are filled in a vessel as shown in the figure. Two small holes are punched at depths h/2 and 3h/2 from the surface of lighter liquid. If v1 and v2 are the velocities of efflux at these two holes, then v1/v2 is
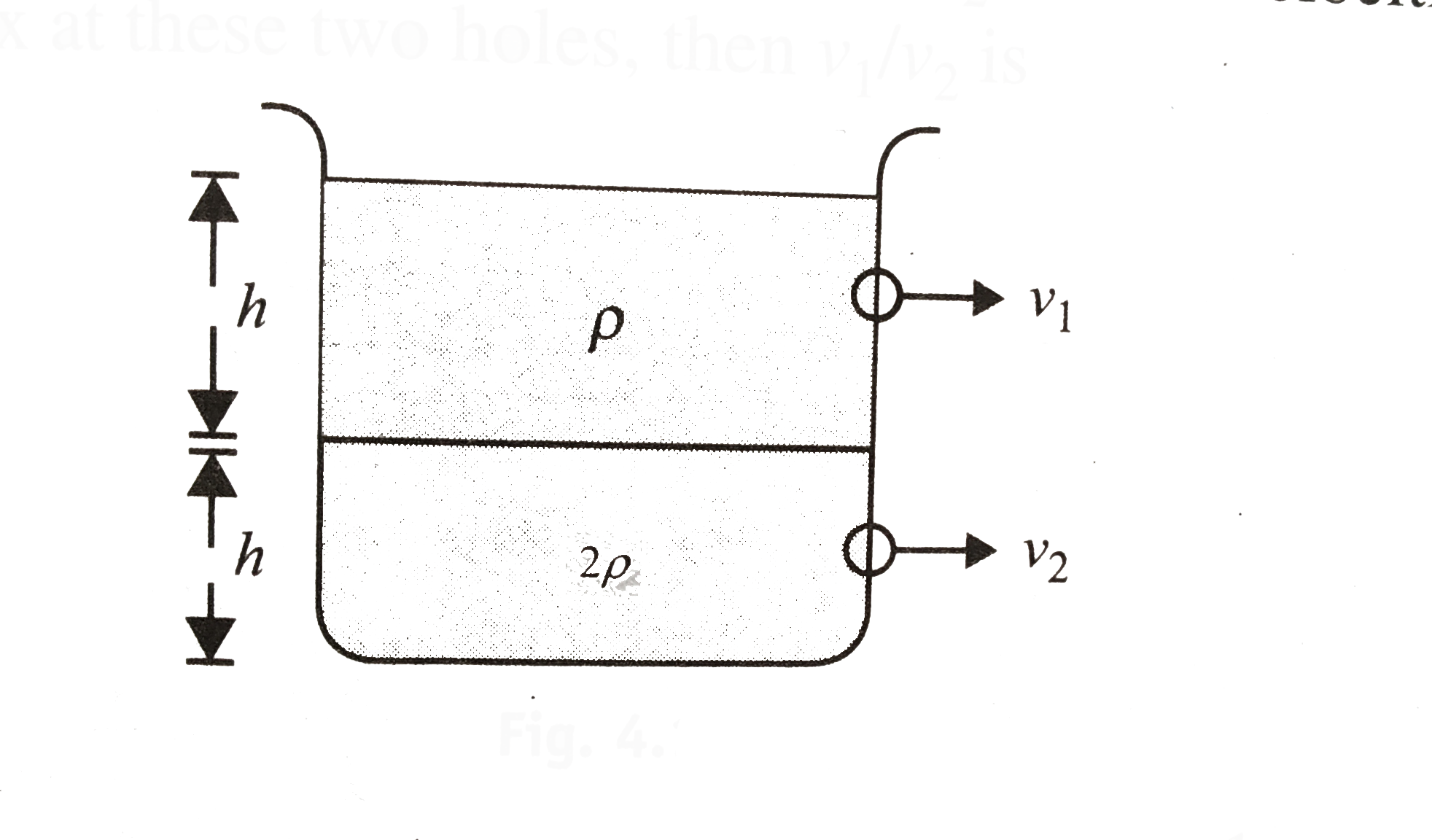 A12√2B12C14D1√2
A12√2B12C14D1√2A beaker is filled with a liquid of density ρ upto a height h If the beaker is at rest, the mean pressure at the walls is:
A0BhρgChρg3D2hρg
Equal volumes of two immiscible liquids of densities ρand2ρ are filled in a vessel as shown in figure. Two small holes are punched at depth h/2 and 3h/2 from the surface of lighter liquid. If v1andv2 are the velocities of efflux at these two holes then (v2v1)2 is
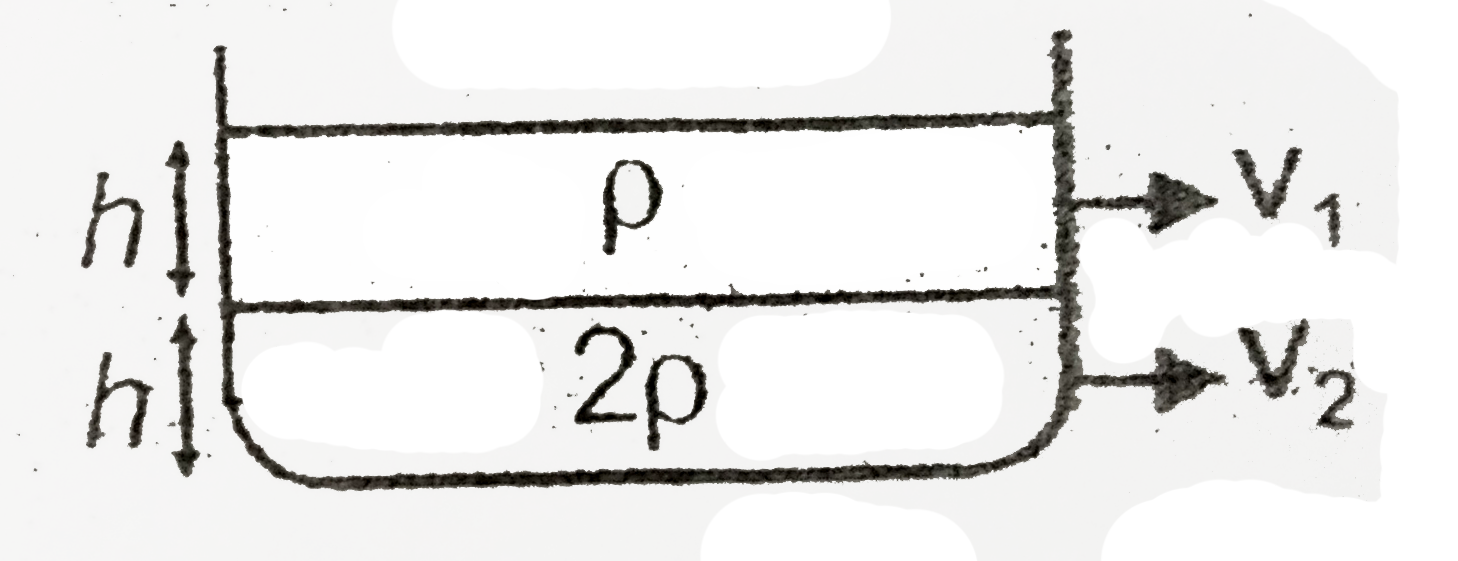
View SolutionEqual volumes of two immiscible liquids of densities ρand2ρ are filled in a vessel as shown in figure. Two small holes are punched at depth h/2 and 3h/2 from the surface of lighter liquid. If v1andv2 are the velocities of efflux at these two holes then (v2v1)2 is
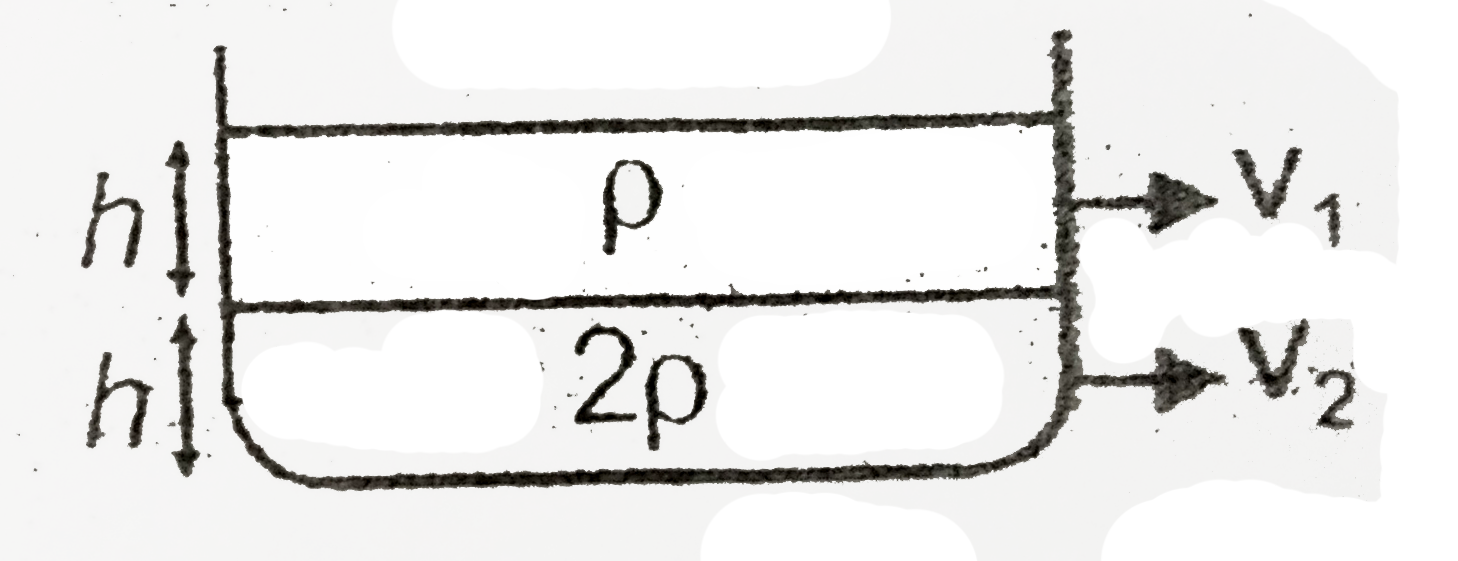
View SolutionEqual volume of two immiscible liquids of densities ρ and 2ρ are filled in a vessel as shown in the figure. Two small holes are punched at depths h/2 and 3h/2 from the surface of lighter liquid. If v1 and v2 are the velocities of efflux at these two holes, then v1/v2 is
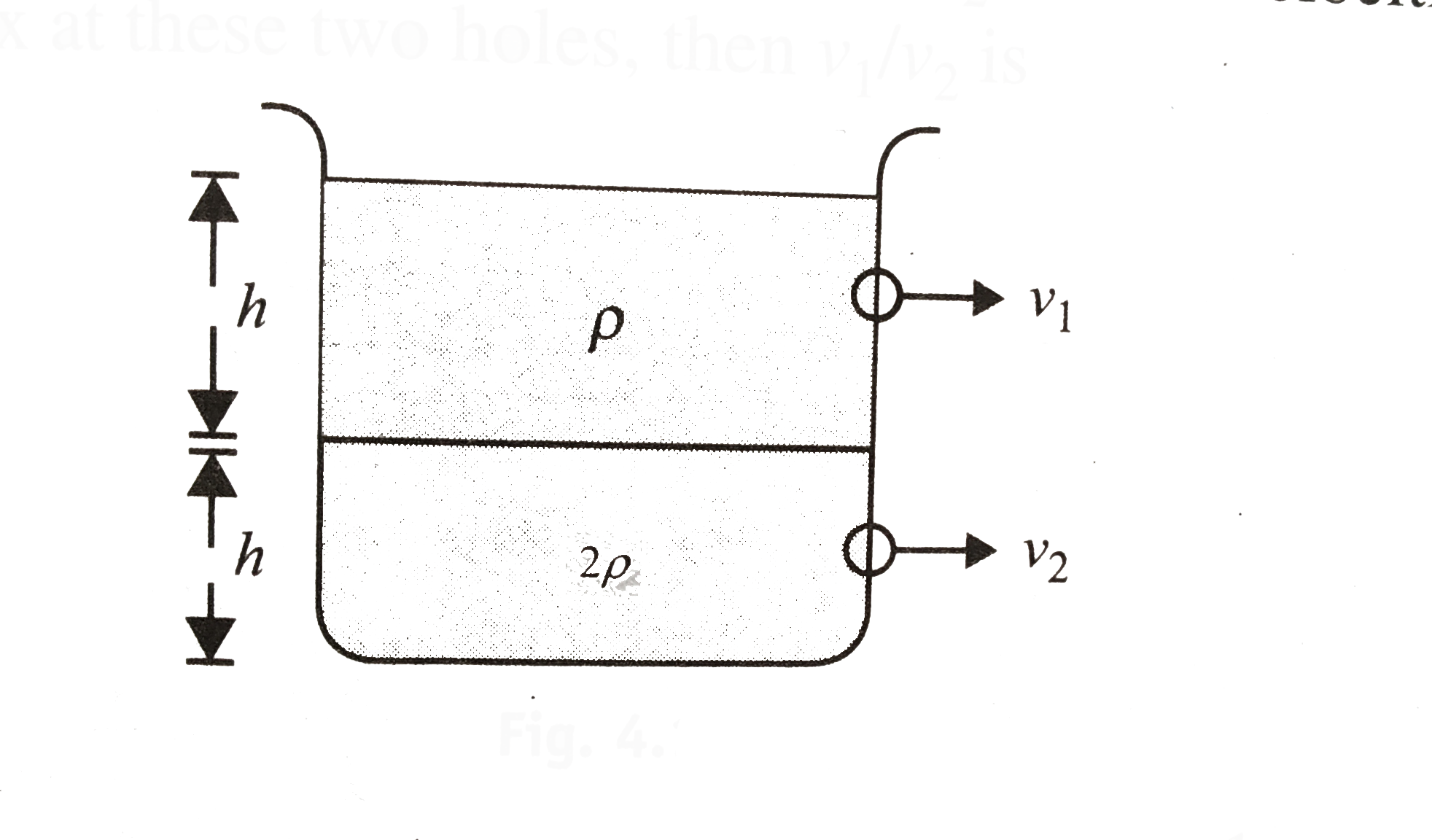
View SolutionEqual volume of two immiscible liquids of densities ρ and 2ρ are filled in a vessel as shown in the figure. Two small holes are punched at depths h/2 and 3h/2 from the surface of lighter liquid. If v1 and v2 are the velocities of efflux at these two holes, then v1/v2 is
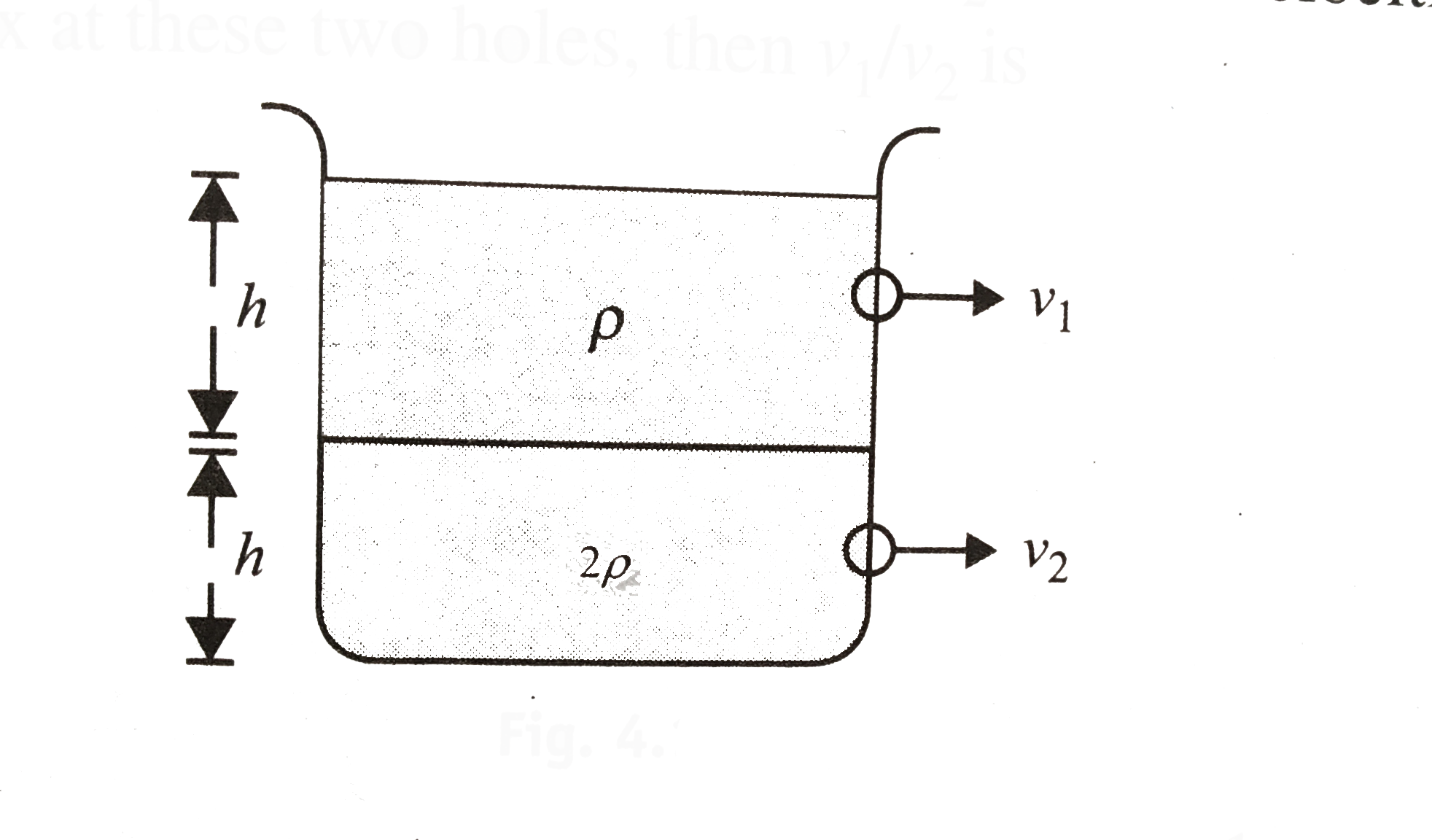
View Solution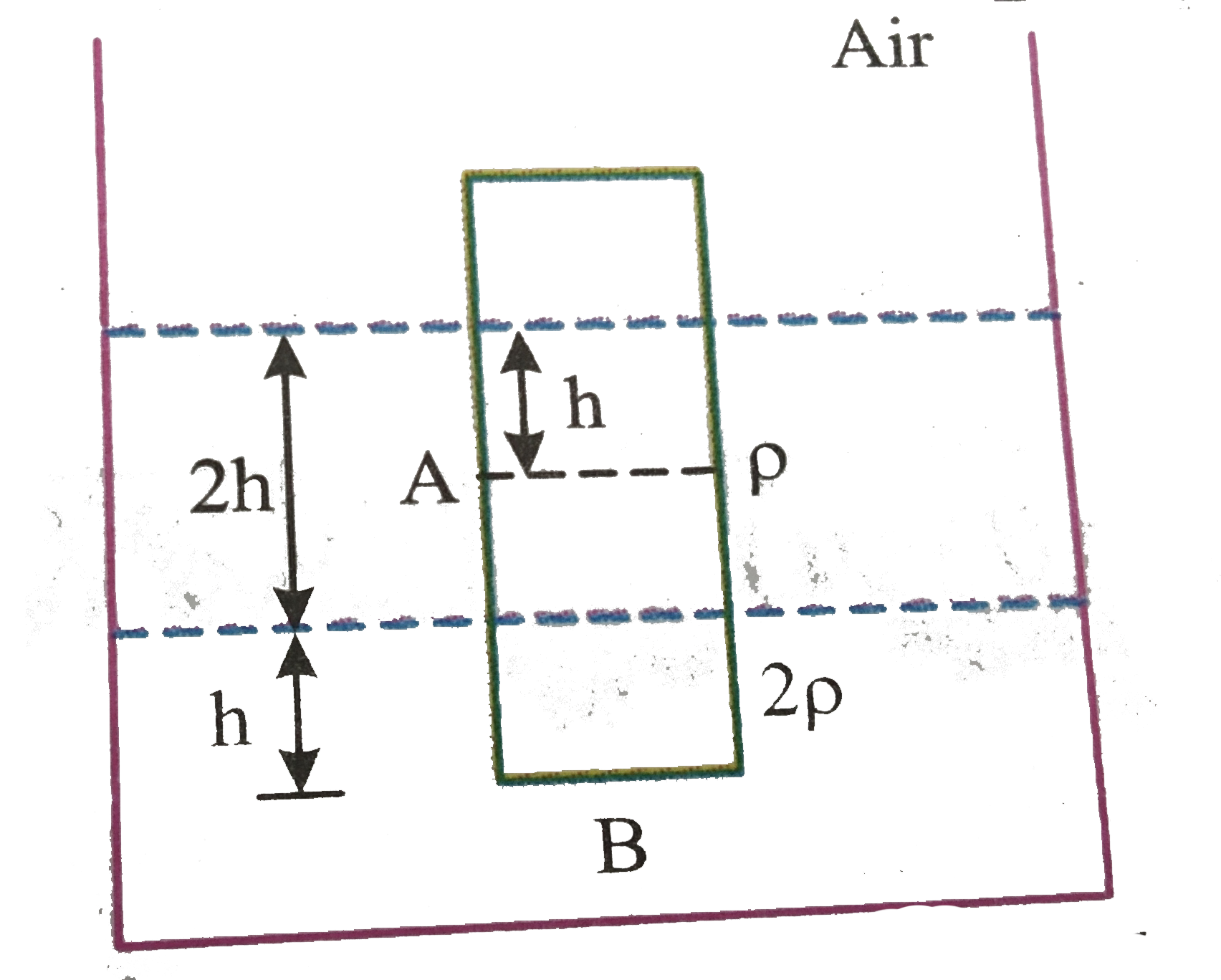
A cylinder stands vertical in two immiscible liquids of densities ρ and 2ρ as shown. Find the difference in pressure at point A and B:
View Solution
