A mass of 2kg is suspended from a fixed point by a wire of length 3m and diameter 0.5 mm. Initially the wire is just unstretched, the mass resting on a fixed support. By how much must the temperature fall if the mass is to be entirely supported by the wire? Given that Y of the wire = 206 G Pa, α=11×10−6/∘C. Solution in Telugu
When the temperature decreases the wire contracts in length and lifts the mass up. But the weight begins to produce a stress and counteracts the contraction produced. Hence the contraction due to cooling is equal to the stretching produced by the weight W.
∴ΔL=WLAY=2×9.8×3π(0.25)2×10−6×206×109
Now the contraction due to cooling
= Lαdθ=3×11×10−6×dθ
Since the contraction due to cooling = extension produced by the weight. On solving dθ=44∘C
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE-IA217videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE-IB68videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE99videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 333videos
THERMODYNAMICS
Similar Questions
The equivalance of two systems in thermal equilibrium is represented by the property of
01:58View Solution(A) : Metals are isotropic solids
( R) : Metals are composed of large number of minute crystals which are randomly oriented resulting in isotropy03:50View SolutionThe centre of mass of two particles with masses 2kg and 6 kg located at (1,1,1), (2,2,1) respectively has the coordinates
02:26View SolutionA bullet of mass 10×10−3 moving with a speed of 20ms−1 hits an ice block (0∘C) of 990g kept at rest on a frictionless floor and gets embedded in it. If ice takes 50% of K.E, the amount of ice melted (in grams) approximately is (J=4.2J/cal) (latent heat of ice=80cal/g)
04:48View Solution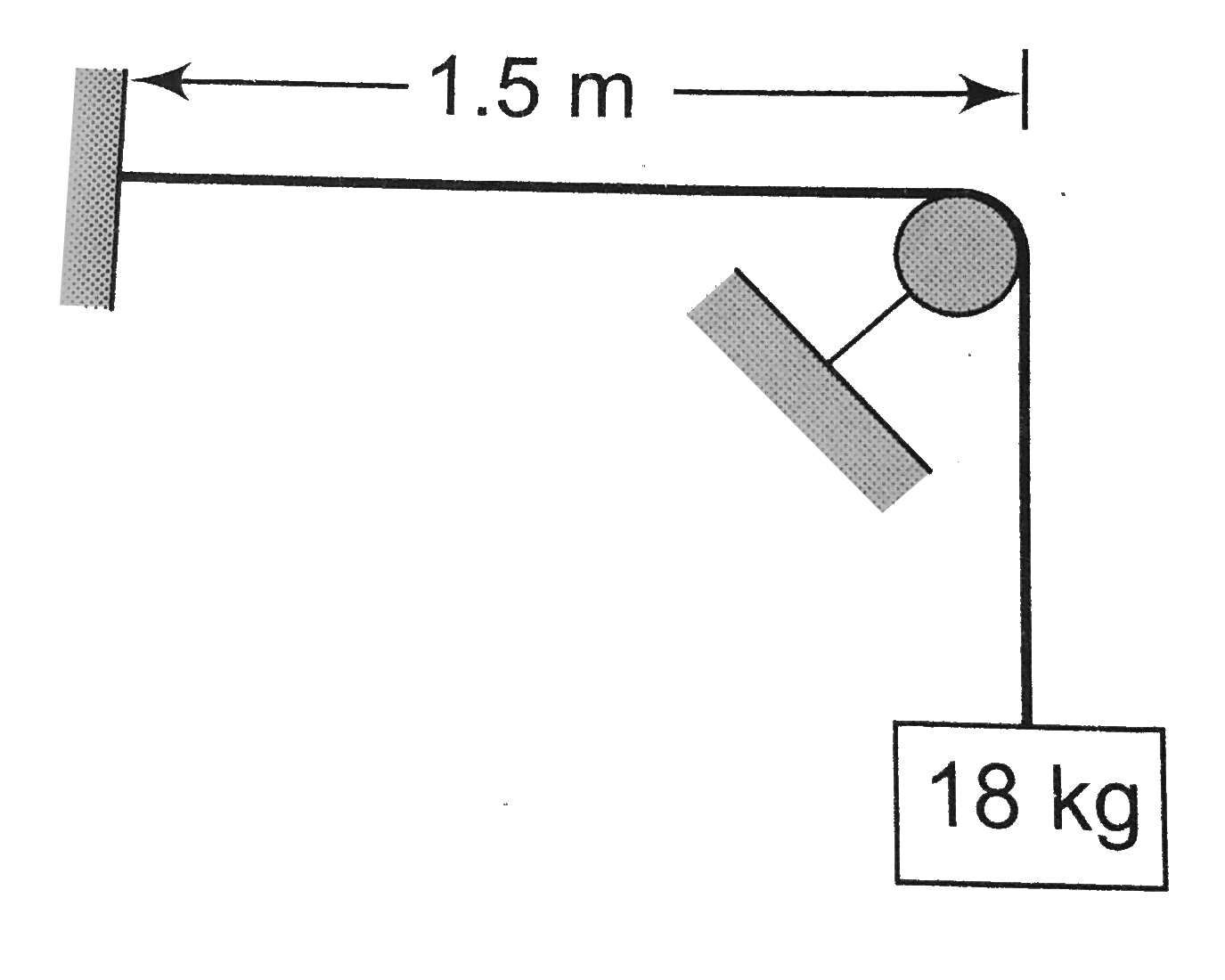
The length of the wire shown in Fig. Between the pulley and fixed support is 1.5m and mass is 12.0g the frequency of vibration with which the wire vibrate two loops leaving the middle point of the wire between the pulleys at rest is03:12View SolutionA mass of 2Kg is suspended from a fixed point by a wire of length 3m and diameter 0.5 mm . Initially the wire is just unstretched, the mass resting on a fixed support. By how much must the temperature fall if the mass is to be entirely supported by the wire (Given Y for wire = 206 G Pa, alpha = 11 xx 10^(-6//@)C )
02:57View SolutionA metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
03:08View SolutionA steel wire 2 mm is diameter is just stretched between two fixed points at a temperature of 20^(@)C . If the temperature falls to 10^(@)C , then the tension in the wire is (Coefficient of linear expansion of steel (alpha) is 11xx10^(-6)//""^(@)C and Y_(s)=2.1xx10^(11)N//m^(2) )
03:06View SolutionA steel wire 2 mm in diameter is just stretched between two fixed points at a temperature of 20^(@)C. If the temperature falls to 10^(@)C, then the tension in the wire is (The coefficient of linear expansion of steel = 11xx10^(-6)//^(@)C and Y for steel 2.1 xx10^(11)N//m^(2))
05:24View SolutionA wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L_1 when mass M is suspended from its free end. The expression for Young's modulus is:
07:54View SolutionFill in the blanks for the sonometer: If the length of the wire and the tension of the wire are doubled and the mass of the wire is fixed in the resonator, the original frequency of the wire will be
03:07View SolutionWhat mass must suspended from the free end of a steel wire of length 2m and diameter 1mm to stretch it by 1mm ? (Y=2×1011Nm−2)
03:56View SolutionA mass of 2kg is suspended from a fixed point by a wire of length 3m and diameter 0.5 mm. Initially the wire is just unstretched, the mass resting on a fixed support. By how much must the temperature fall if the mass is to be entirely supported by the wire? Given that Y of the wire = 206 G Pa, α=11×10−6/∘C.
02:11View SolutionA steel wire 2 mm in diameter is just stretched between two fixed points at a temperature of 20∘C. If the temperature falls to 10∘C, then the tension in the wire is (The coefficient of linear expansion of steel = 11×10−6/∘C and Y for steel 2.1×1011N/m2)
02:57View SolutionA wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
View Solution
