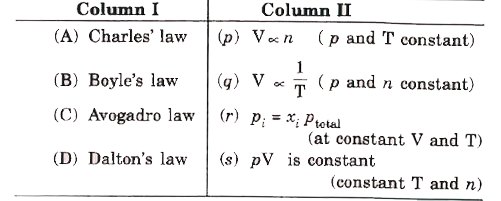In column-l, the projection of a particle moving along a circle (uniformly) in x-y plane with its centre of origin along x and y axes, while in Column-II, the description of particle's motion is given. It is given that particle's angular velocity is constant and equal to ω and the radius of circle is A,δ≠0,π2orπ For this situation match the column-I with column-II
Column - IColumn - IIA) x(t)=Asin(ωt+δ−π2),y(t)=Asin(ωt+δ)P) Uniform circular motion (clockwise)B) x(t)=Asin(ωt+δ),y(t)=Asin(ωt+δ+π2)Q) Uniform circular motion(anti - clockwise)C) x(t)=Asin(ωt),x(t)=Acos(ωt)R) At = 0 particle is neither on x - axis nor on y - axisD) x(t)=Acos(ωt+δ),y(t)=Acos(ωt+δ+π2)S) At t = 0 particle is either on x - axis on y - axis
Text Solution
The correct Answer is:A-PQR ; B - PQR; C-PQR ; D-S
|
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - AAKASH SERIESCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - PRACTICE SHEET (EXERCISE - III)(LEVEL - II)(STRIGHT OBJECTIVE TYPE QUESTIONS)
12 Videos
- SIMPLE HARMONIC MOTION BOOK - AAKASH SERIESCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - PRACTICE SHEET (EXERCISE - III)(LEVEL - II)(MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
3 Videos
- SIMPLE HARMONIC MOTION BOOK - AAKASH SERIESCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - PRACTICE SHEET (EXERCISE - II)(LEVEL - II)(LINKED COMPREHENSION TYPE QUESTIONS)
3 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
- SURFACE TENSIONBOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS )
8 Videos
Similar Questions
Knowledge Check
Match item in column I with those given in column II. Column 1
 AA-V, B-IV, C-III, D-I, E-IIBA-IV, B-V, C-II, D-I, E-IICA-IV, B-V, C-III, D-II, E-IDA-V, B-III, C-I, D-II, E-IV
AA-V, B-IV, C-III, D-I, E-IIBA-IV, B-V, C-II, D-I, E-IICA-IV, B-V, C-III, D-II, E-IDA-V, B-III, C-I, D-II, E-IVMatch the process given in column I with its description given in column II.
 A(i)-(C) , (ii)-(D), (iii)-(B), (iv)-(A)B(i)-(B) , (ii)-(A), (iii)-(C), (iv)-(D)C(i)-(C) , (ii)-(A), (iii)-(B), (iv)-(D)D(i)-(C) , (ii)-(D), (iii)-(B), (iv)-(A)
A(i)-(C) , (ii)-(D), (iii)-(B), (iv)-(A)B(i)-(B) , (ii)-(A), (iii)-(C), (iv)-(D)C(i)-(C) , (ii)-(A), (iii)-(B), (iv)-(D)D(i)-(C) , (ii)-(D), (iii)-(B), (iv)-(A)
Match the solution given in column I and the colours given in column II

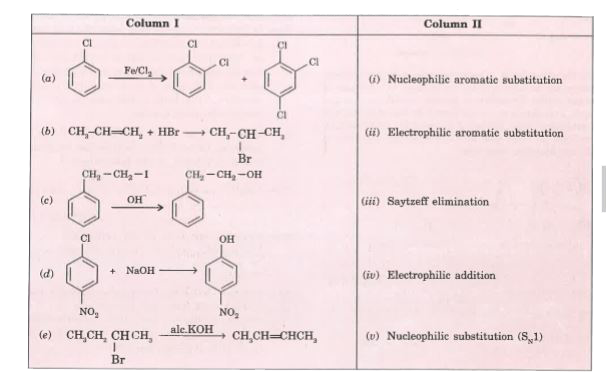
View SolutionMatch the reactions given in Column I with the types of reactions given in Column II.
View SolutionA particle is moving along a circle of a fixed radius and gaining speed in a uniform manner. Mathc columns I and II.

View SolutionMatch the reactions given in Column I with the types of reactions given in Column II.

View SolutionMatch the column-I to value of Tension given in column-II, assuming mass of particle equal to m

View SolutionMatch the terms in column -I with their description in column -II and choose the correct option :

View Solution