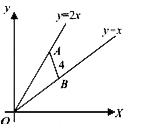
Let AB be a line segment of length 4 with A on the line y=2x and B on the line y=x. The locus of the middle point of the line segment is
25x2+13y2+36xy−4=0
25x2+13y2−36xy−4=0
13x2+25y2−36xy−4=0
13x2+25y2+36xy−4=0
The correct Answer is:B
Let B=(α,α) and middle point AB is (h,k)
Then, A≡(2h−α,2k−α)
Lies on y=2x
Then, (2k−α)=2(2h−α)∴α=4h−2k
|AB|=4⇒√(2h−2α)2+(2k−2α)2=4
or(h−α)2+(k−α)2=4or[h−(4h−2k)]2+[k−(4h−2k)]2=4
⇒(−3h+2k)2+(−4h+3k)2=4or25h2+13k2−36hk=4
Required locus is 25x2+13y2−36xy−4=0
Similar Questions
If P is point on the parabola y2=8xandA is the point (1,0), then the locus of the mid point of the line segment AP is
View Solutioncuts(d) χ 2 + y 2 + 4x-6y + 9-0n ofline y-2x and Bon. the line y = χ. The lot、A on tmiddle point of the line segment is(164 Let AB be a line segment of length 4 wthelocus of the(b) a pair of lines(d) none of these(a) a line(c) a circle1a The locus of the centre of a circle which touch
View Solution
Knowledge Check
Let AB be a line segment of length 4 with A on the line y=2x and B on the line y=x. The locus of the middle point of the line segment is
A25x2+13y2+36xy−4=0B25x2+13y2−36xy−4=0C13x2+25y2−36xy−4=0D13x2+25y2+36xy−4=0If the extremities of a line segment of length l moves in two fixed perpendicular straight lines, then the locus of the point which divides this line segment in the ratio 1 : 2 is-
Aa parabolaBan ellipseCa hyperbolaDNone of these
A line segment AB of length a moves with its ends on the axes.The locus of the point P which divides the segment in the ratio 1:2 is
View SolutionA straight line segment of length / moves with its ends axis and y-axis. The locus of the point which x-axis and y-a divides the line segment in the ratio 1: 2 18s on
View Solutiony2=4ax is a parabola . A line segment joining focus of parabola to any moving point (at2,2at) is made . Then locus of mid-point of the line segment is a parabola with the directrix
View SolutionA straight line segment of length/moves with its ends on two mutually perpendicular lines. Find the locus of the point which divides the line segment in the ratio 1:2
View Solutiony=mx be a variable line (m is variable) intersect the lines 2x+y−2=0 and x−2y+2=0 in P and Q.The locus of midpoint of segment of PQ is
View SolutionA line segment AB of length '2' moves with its ends on the axes. The locus of the point P which divides the segment in the ratio 1:1 is
View Solution
