If $f (x) = \sqrt{{cosec}^{2} x - 2 sin x cos x - \frac{1}{{tan}^{2} x}} x \in (\frac{7 π}{4}, 2 π)$ , then $f . (\frac{11 π}{6}) =$

A

$\frac{1 - \sqrt{3}}{2}$

B

$\frac{\sqrt{3} - 1}{2}$

C

$\frac{1 + \sqrt{3}}{2}$

D

None of these

Text Solution

Verified by Experts

The correct Answer is:A

$f (x) = \sqrt{{cosec}^{2} x - {cot}^{2} x - 2 sin x cos x}$
$= \sqrt{{(cos x - sin x)}^{2}}$

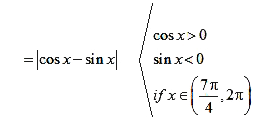
f(x)=cos x -sin x
$\Rightarrow$ f.(x)=-sin x - cos x
$f . (\frac{11 π}{6}) = - [\frac{sin (11 π)}{6} + \frac{cos (11 π)}{6}]$
$\Rightarrow f . (\frac{11 π}{6}) = - [\frac{- 1}{2} + \frac{\sqrt{3}}{2}] = \frac{1 - \sqrt{3}}{2}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
If $f (x) = \sqrt{cos e c^{2} x - 2 sin x cos x - \frac{1}{{tan}^{2} x}}$
$x \in (\frac{7 π}{4}, 2 π)$ then $f' (\frac{11 π}{6}) =$
A $\frac{1 - \sqrt{3}}{2}$
B $\frac{\sqrt{3} - 1}{2}$
C $\frac{1 + \sqrt{3}}{2}$
DNone of these
Question 2 - Select One
If $f (x) = \frac{1 - cos x}{1 - sin x}, then: f' (\frac{π}{2})$ is
A1
B0
C $\infty$
Dindeterminate
Question 3 - Select One
If $f (x)$ is contiuous at $x = \frac{π}{2}$ , where $f (x) = \frac{cos e c x - sin x}{\frac{π}{2} - x}, for x \neq \frac{π}{2}$ , then $f (\frac{π}{2}) =$
A $\frac{1}{4}$
B0
C $\frac{1}{6}$
D $\frac{1}{8}$

Recommended Questions

Home
Ask Doubt
Profile