FAOR: Dynamics (torgue equation about hinge) | Conservation of energy | FAOR problems: hinged rod | Hinge force calculation | Fixed pulley
Step by step video solution for FAOR: Dynamics (torgue equation about hinge) | Conservation of energy | FAOR problems: hinged rod | Hinge force calculation | Fixed pulley by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Angular momentum of a particle | Angular momentum of a rigid body in pure translation | FAOR | GRBM-General Rigid Body Motion | Torgue and angular momentum relation | Application of conservation of angular momentum | Rod particle collisions
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
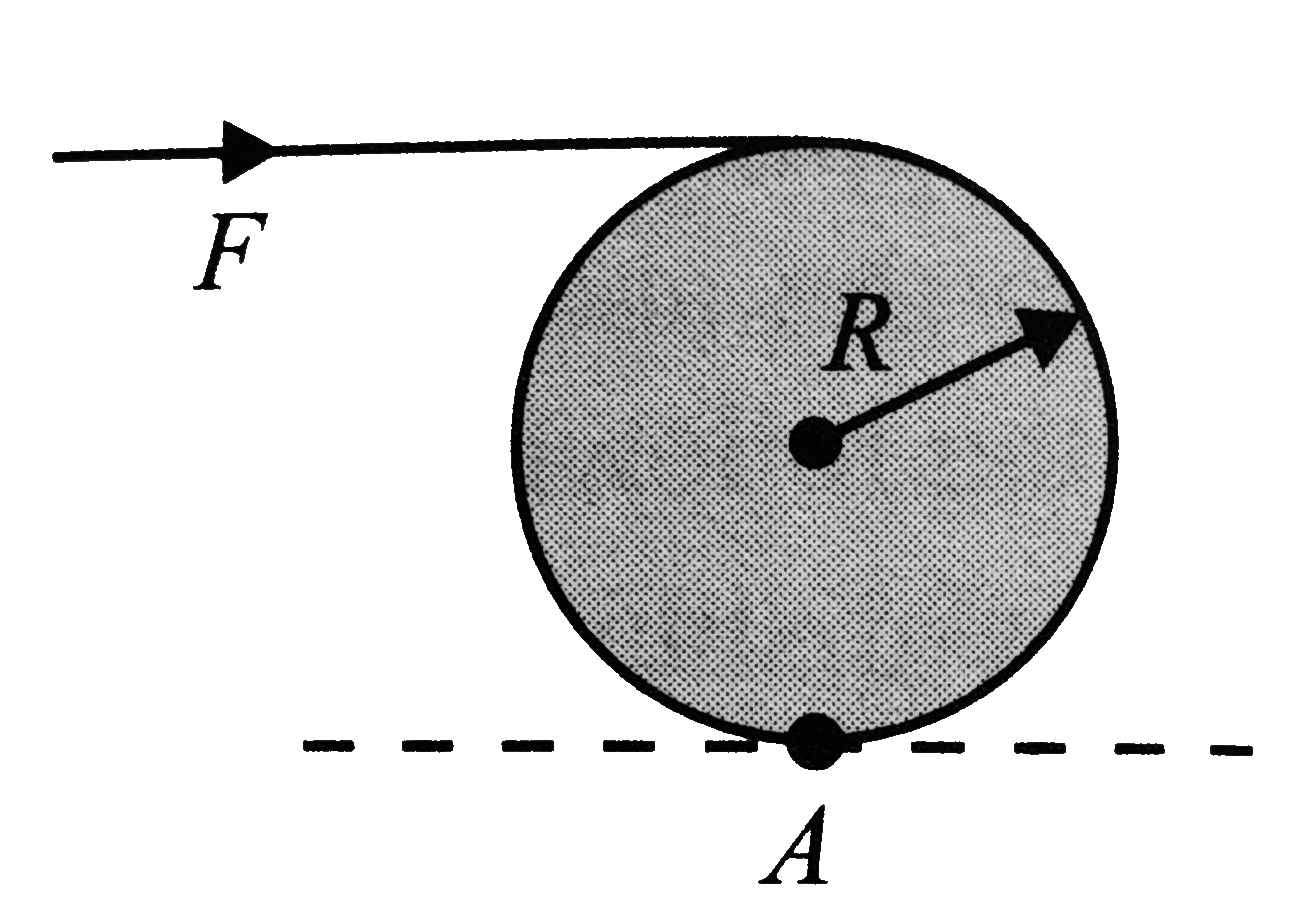
Component of reaction at the hinge in the horizontal direction is
View Solution
Knowledge Check
In previous problem, what is the reaction force on the hinge ?
AW−P upwardBW−P downwardCW−P to the leftDNone of theseTwo particle of mass m each are fixed to a massless rod of length 2l . The rod is hinged at one end about a smooth hinge and it performs oscillations of small angle in vertical plane. The length of the equivalent simple pendulum is:
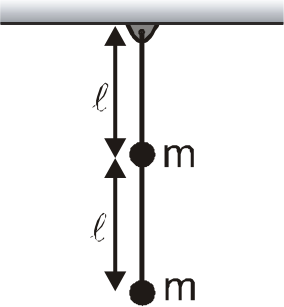A3l2B10l3C5l3DNone of theseA rod of mass 'm' and length 'l' is hinged at point 'P ' and rod can rotate about higne point 'P' in vertical plane. Other end of rod is connected through a block by a string which is passed through pulley of mass 'm' and radius 'R' and there is no slipping between the pulley and the string as shown in figure. At t=0, system is released . Find the hinge reaction at P at t=0.
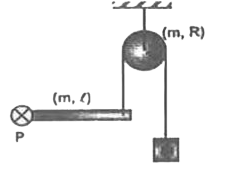A211mgB411mgC611mgD811mg
When a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
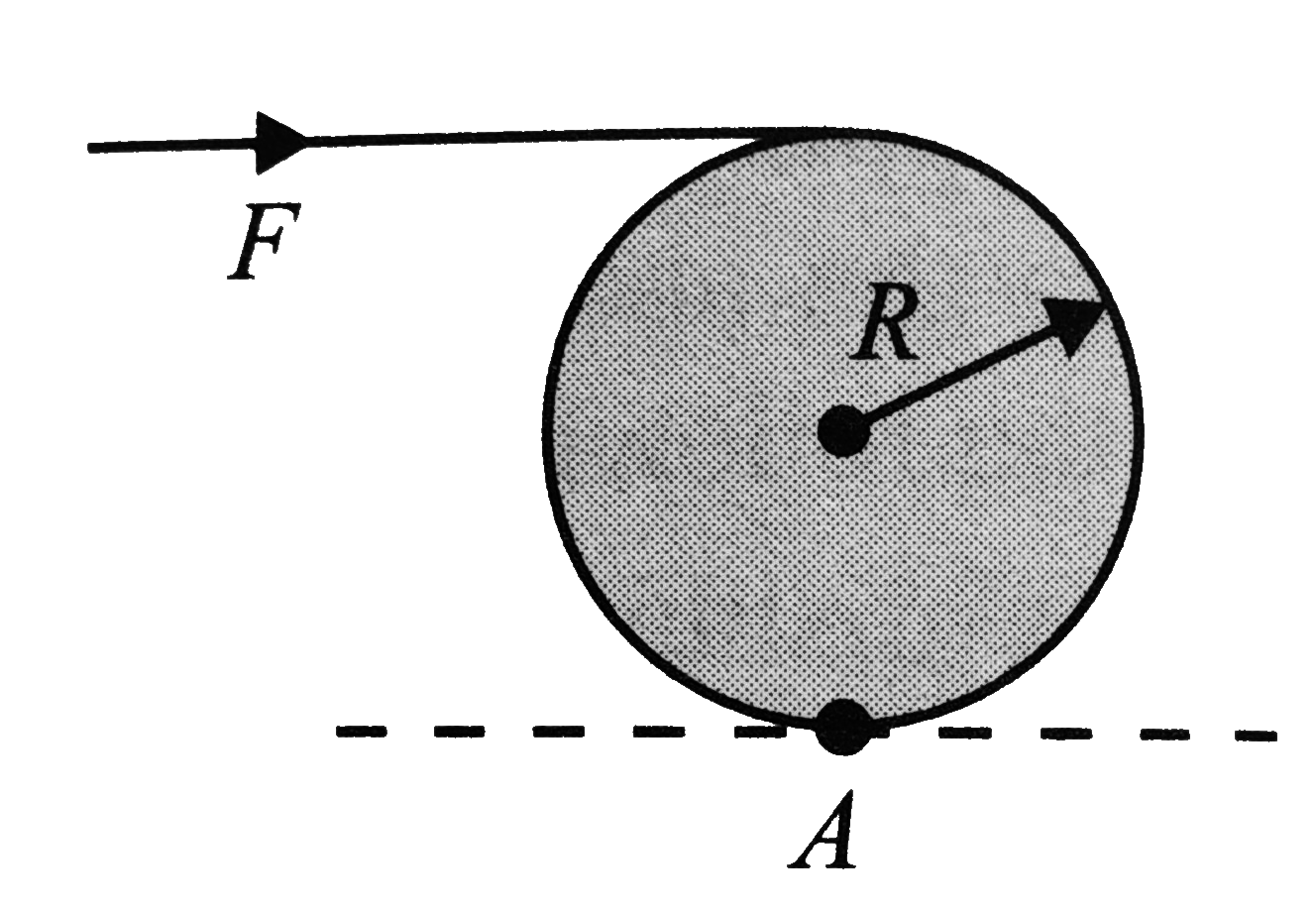
Component of reaction at the hinge in the vertical direction is
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
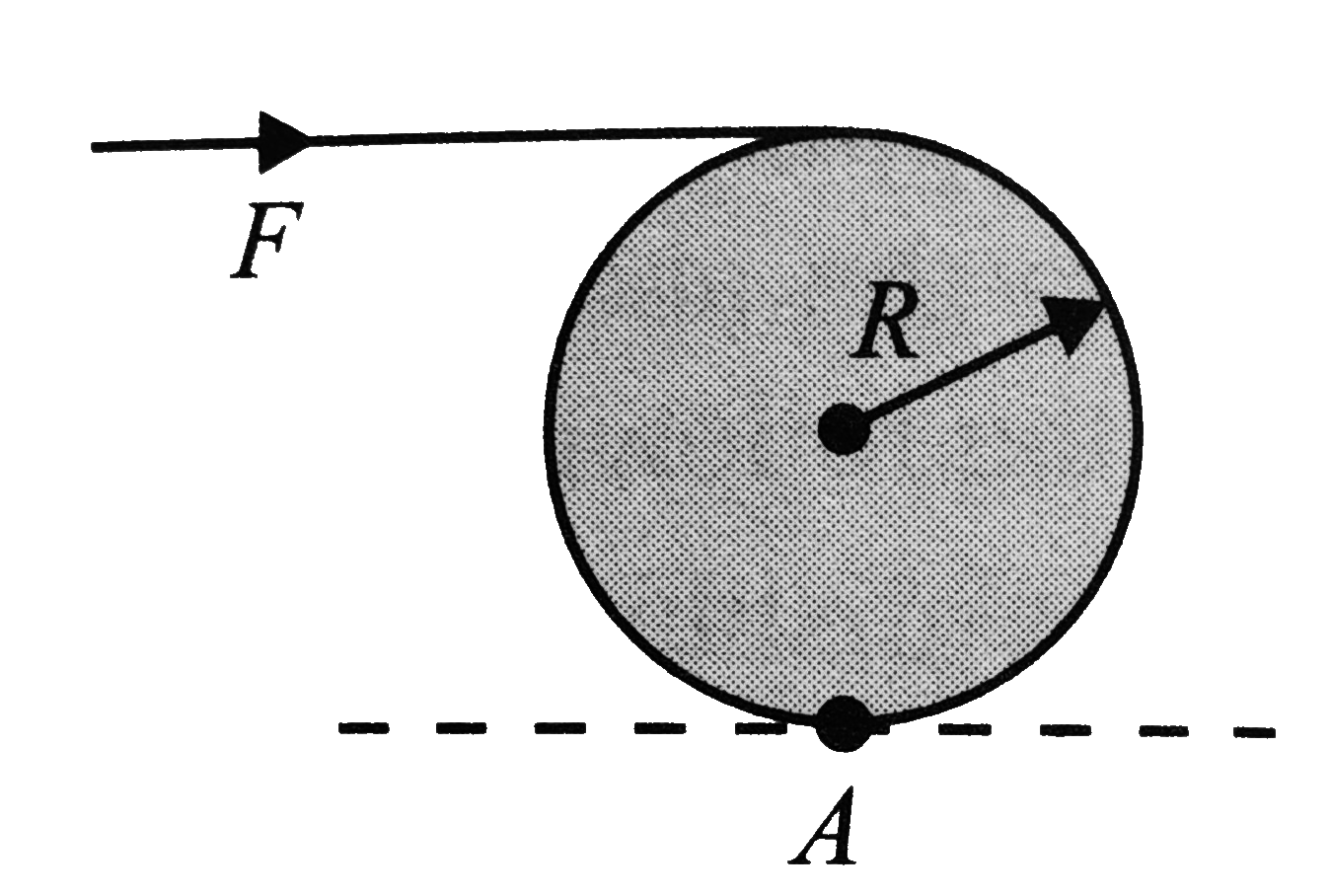
Tangential acceleration of the centre of mass is
View SolutionA uniform rod mass m and length L is free to rotate about hinge O. A slight disturbance cause the rod to rotate freely about O and it strikes the ground.
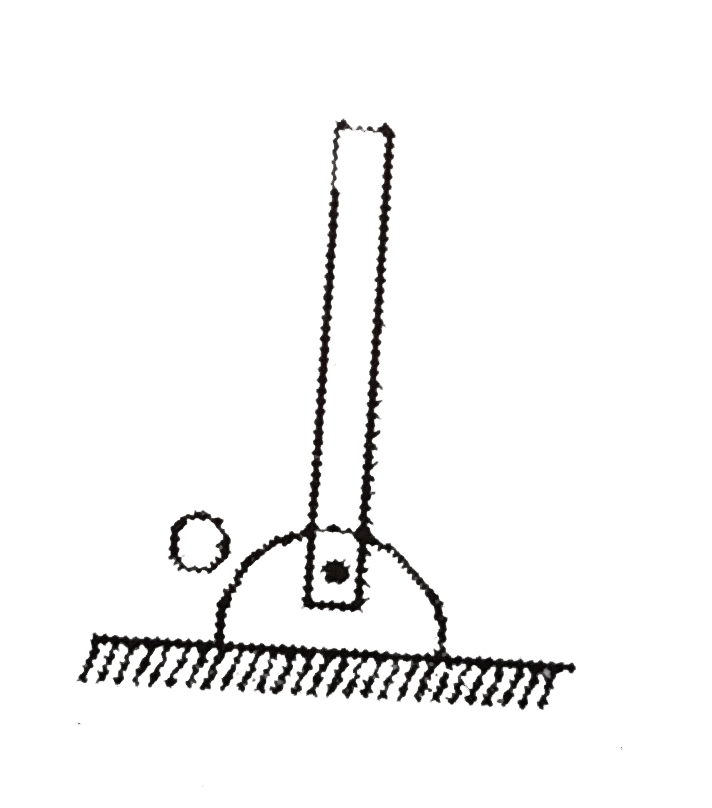
Horizontal force applied on rod by hinge just before the rod hits the surface is:
View SolutionA uniform rod of mass M=2kg and length L is suspended by two smooth hinges 1 and 2 as shown in Fig. A force F=4N is applied downward at a distance L/4 from hinge 2. Due to the application of force F, hinge 2 breaks. At this instant, applied force F is also removed. The rod starts to rotate downward about hinge 1. (g=10m/s2)
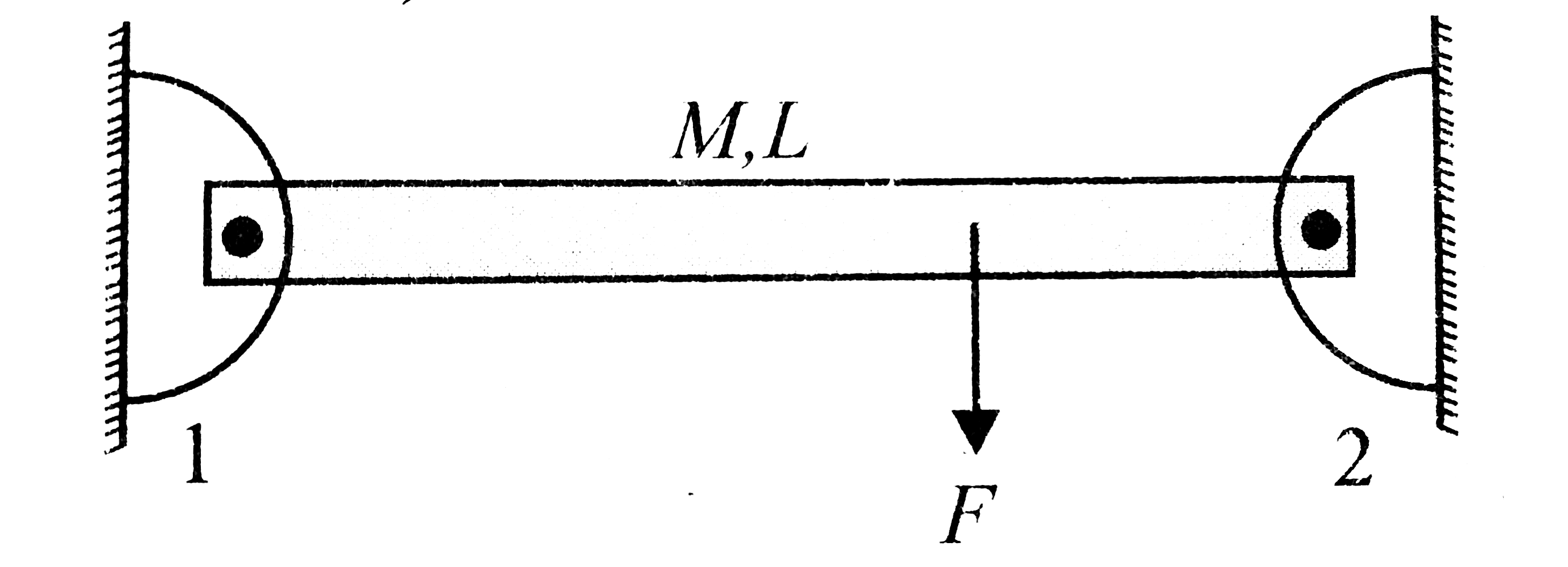
The acceleration of the end point of the rod of small mass dm at the end point of the rod, when the rod becomes vertical is
View SolutionConsider the situation shown in the figure. Uniform rod of length L can rotat freely about the hinge A in vertical plane. Pulleys and stringa are light and frictionless. If the rod remains horizontal at rest when the system is released then the mass of the rod is
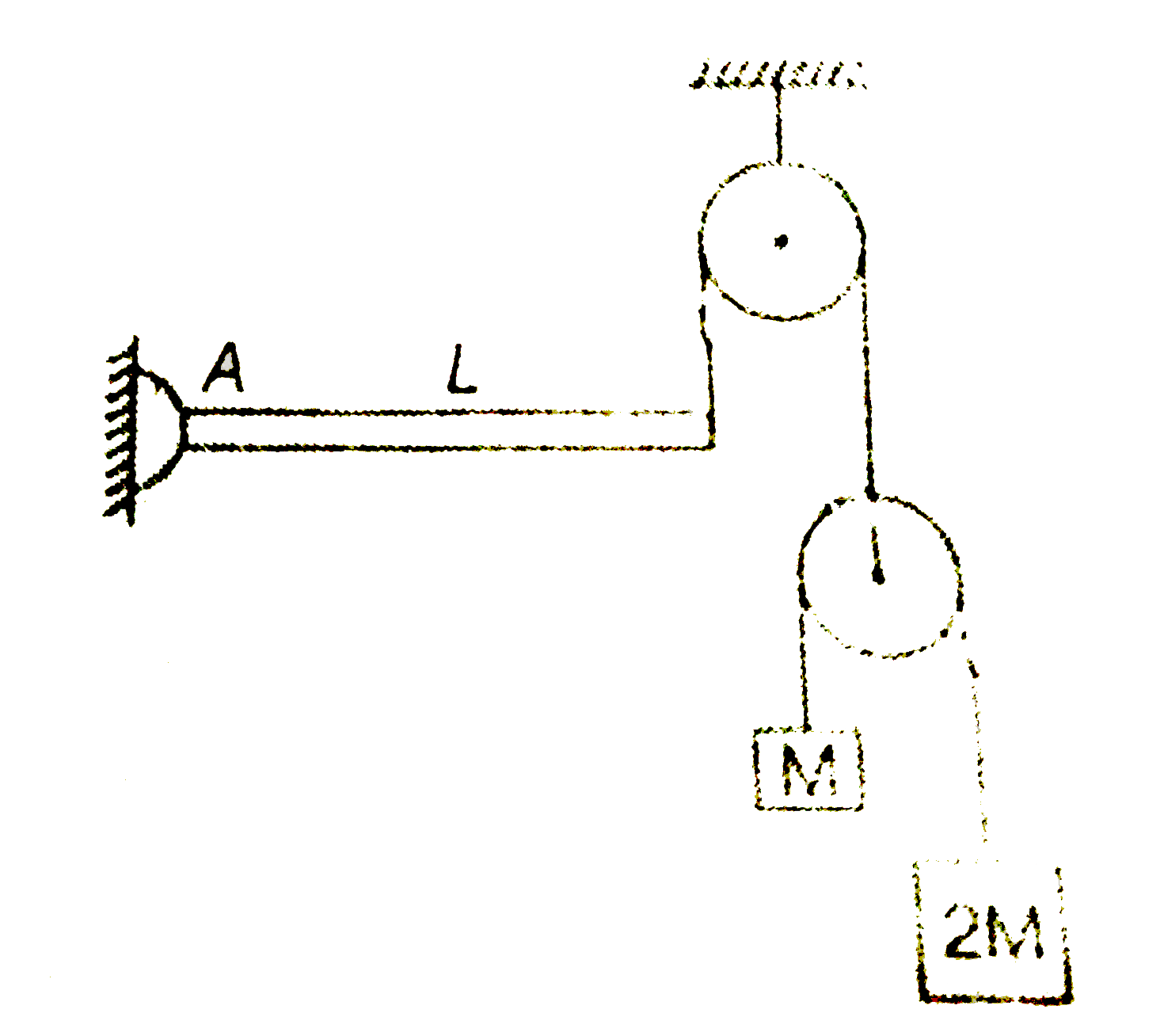
View Solution