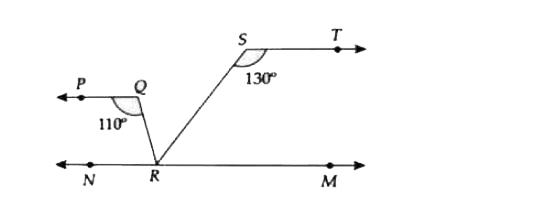
In the given figure, if PQ∣∣ST,∠PQR=110∘ and ∠RST=130∘, then find ∠QRS.
The correct Answer is:∠QRS=60∘
To solve the problem, we need to find the measure of angle QRS given that PQ is parallel to ST, angle PQR is 110°, and angle RST is 130°.
1. Identify the Given Information:
- PQ || ST (PQ is parallel to ST)
- ∠PQR = 110°
- ∠RST = 130°
2. Draw a Parallel Line:
- Draw a line MN parallel to ST. This gives us three parallel lines: PQ, ST, and MN.
3. Use the Property of Parallel Lines:
- Since PQ is parallel to MN, the sum of the interior angles on the same side of the transversal (line QR) must equal 180°.
- Therefore, we can write the equation:
∠PQR+∠MRQ=180°
4. Substitute the Known Angle:
- Substitute the value of ∠PQR into the equation:
110°+∠MRQ=180°
5. Solve for ∠MRQ:
- Rearranging the equation gives:
∠MRQ=180°−110°=70°
6. Use the Other Parallel Line Property:
- Now, since ST is parallel to MN, we can apply the same property:
∠RST+∠NRS=180°
7. Substitute the Known Angle:
- Substitute the value of ∠RST into the equation:
130°+∠NRS=180°
8. Solve for ∠NRS:
- Rearranging gives:
∠NRS=180°−130°=50°
9. Apply the Linear Pair Property:
- Now, consider the angles along line MN:
∠QRM+∠QRS+∠SRN=180°
- Substitute the known angles:
70°+∠QRS+50°=180°
10. Solve for ∠QRS:
- Combine the known angles:
120°+∠QRS=180°
- Rearranging gives:
∠QRS=180°−120°=60°
Final Answer:
∠QRS=60°
- PQ || ST (PQ is parallel to ST)
- ∠PQR = 110°
- ∠RST = 130°
- Draw a line MN parallel to ST. This gives us three parallel lines: PQ, ST, and MN.
- Since PQ is parallel to MN, the sum of the interior angles on the same side of the transversal (line QR) must equal 180°.
- Therefore, we can write the equation:
∠PQR+∠MRQ=180°
- Substitute the value of ∠PQR into the equation:
110°+∠MRQ=180°
- Rearranging the equation gives:
∠MRQ=180°−110°=70°
- Now, since ST is parallel to MN, we can apply the same property:
∠RST+∠NRS=180°
- Substitute the value of ∠RST into the equation:
130°+∠NRS=180°
- Rearranging gives:
∠NRS=180°−130°=50°
- Now, consider the angles along line MN:
∠QRM+∠QRS+∠SRN=180°
- Substitute the known angles:
70°+∠QRS+50°=180°
- Combine the known angles:
120°+∠QRS=180°
- Rearranging gives:
∠QRS=180°−120°=60°
∠QRS=60°
Topper's Solved these Questions
- LINE AND ANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINE AND ANGLESEXERCISE - EXERCISE 6.3
6 Videos
- LINE AND ANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINE AND ANGLESEXERCISE - Sums of Enrich Remember.s
8 Videos
- LINE AND ANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINE AND ANGLESEXERCISE - Multiple Choice Questions MCQs)
10 Videos
- INTRODUCTION TO EUCLID.S GEOMETRYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - INTRODUCTION TO EUCLID.S GEOMETRYEXERCISE - MULTIPLE CHOICE QUESTIONS
3 Videos
- PROBABILITY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - Multiple Choice Questions (MCQs)
10 Videos
Similar Questions
Knowledge Check
In the given figure, PQ = ____.
 AMNBLMCLNDQR
AMNBLMCLNDQRIn the given figure, if OP||Rs,∠OPQ=110∘and∠QRS=130∘,then∠PQR is equal to
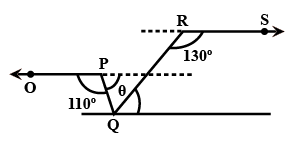 A40∘B50∘C60∘D70∘
A40∘B50∘C60∘D70∘
In the given figure , ¯¯¯¯¯¯¯LM∣∣¯¯¯¯¯¯NO,∠QMR=50∘ and ∠RSO=110∘. Find ∠MRQ.A60∘B70∘C80∘D50∘
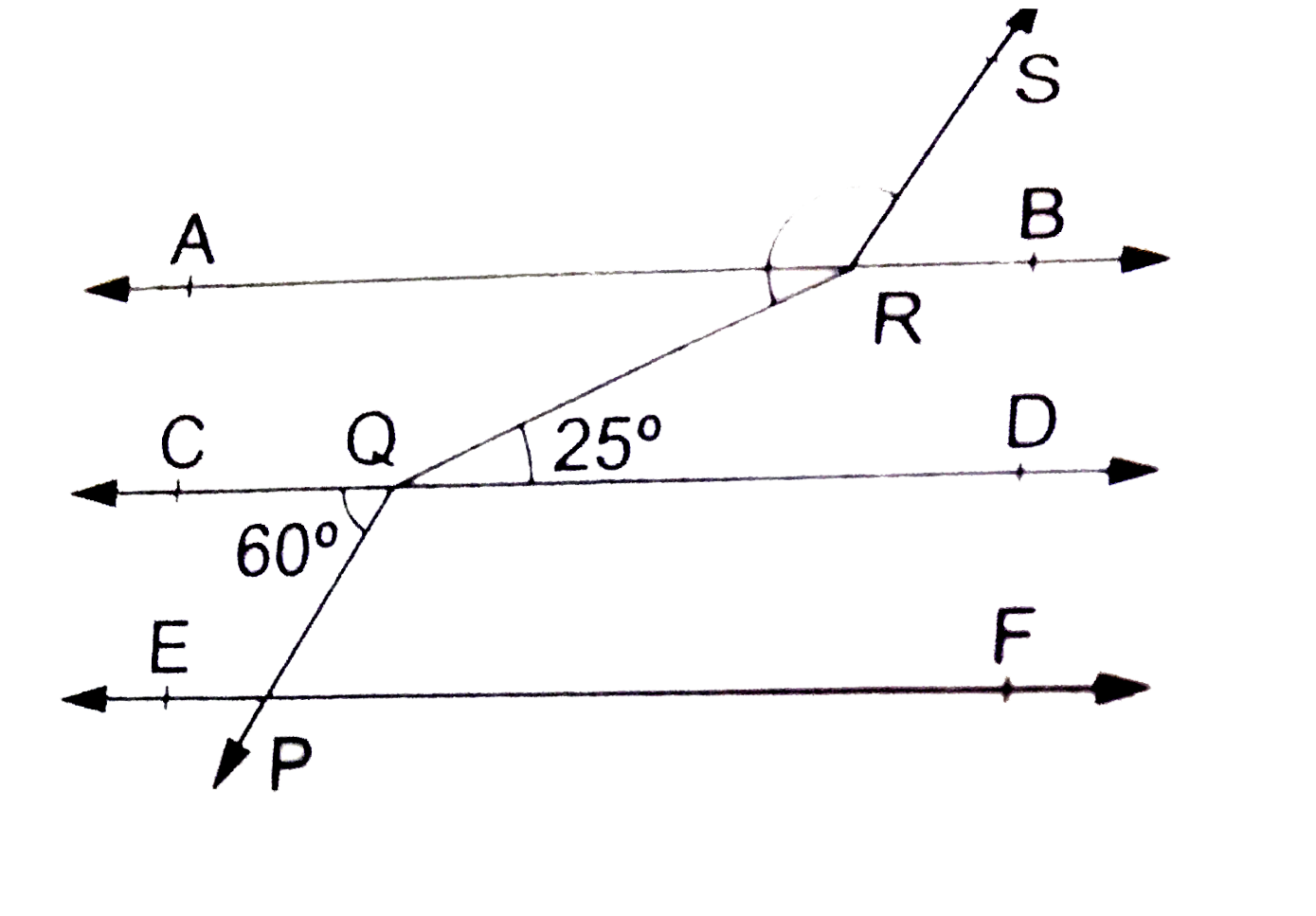
In the given figure, AB||CD||EF,PQ∣∣RS,∠RQD=25∘ and ∠CQP=60∘. Find ∠QRS.
View SolutionIn the given figure, ∠OAB=110∘ and ∠BCD=130∘ then ∠ABC is equal to
View SolutionIn the adjoining figure, if ∠PQR=90∘,∠PSR=90∘,then find PR and RS.

View Solution
In the figure, PQ=QR,∠RPQ=60∘,and∠QRS=20∘. Find the measure of ∠QSR.
View SolutionIn the given figure, if AB∣∣CD,∠APQ=60∘and∠PRD=130∘ find 'x'and'y' and write the conjugate angles for that.
View Solution