Ray EX is the bisector of and ray EY is the bisector of . If , then find and .
The correct Answer is:
To solve the problem step by step, we will use the information given about the angles and their bisectors.
1. Identify Given Information:
- Ray EX is the bisector of angle DEF.
- Ray EY is the bisector of angle DEX.
- Angle DEX = 42°.
2. Determine Angle DEX:
- Since ray EY bisects angle DEX, we can find the two equal parts of angle DEX.
- Angle DEX = 42° means:
Angle YEX=Angle FEX=Angle DEX2=42°2=21°.
3. Determine Angle DEF:
- Since ray EX bisects angle DEF, we can express angle DEF in terms of angle DEX.
- Angle DEF is composed of two equal angles, which are angle DEX and angle FEX.
- Therefore, we have:
Angle DEF=Angle DEX+Angle FEX=42°+42°=84°.
4. Determine Angle YEF:
- Angle YEF is made up of angle YEX and angle FEX.
- We already know:
- Angle YEX = 21° (from step 2)
- Angle FEX = 42° (since it is equal to angle DEX).
- Therefore:
Angle YEF=Angle YEX+Angle FEX=21°+42°=63°.
5. Final Answers:
- Angle DEF = 84°.
- Angle YEF = 63°.
Summary of Results:
- Angle DEF = 84°.
- Angle YEF = 63°.
- Ray EX is the bisector of angle DEF.
- Ray EY is the bisector of angle DEX.
- Angle DEX = 42°.
- Since ray EY bisects angle DEX, we can find the two equal parts of angle DEX.
- Angle DEX = 42° means:
Angle YEX=Angle FEX=Angle DEX2=42°2=21°.
- Since ray EX bisects angle DEF, we can express angle DEF in terms of angle DEX.
- Angle DEF is composed of two equal angles, which are angle DEX and angle FEX.
- Therefore, we have:
Angle DEF=Angle DEX+Angle FEX=42°+42°=84°.
- Angle YEF is made up of angle YEX and angle FEX.
- We already know:
- Angle YEX = 21° (from step 2)
- Angle FEX = 42° (since it is equal to angle DEX).
- Therefore:
Angle YEF=Angle YEX+Angle FEX=21°+42°=63°.
- Angle DEF = 84°.
- Angle YEF = 63°.
- Angle DEF = 84°.
- Angle YEF = 63°.
Topper's Solved these Questions
- LINE AND ANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINE AND ANGLESEXERCISE - Multiple Choice Questions MCQs)
10 Videos
- LINE AND ANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINE AND ANGLESEXERCISE - Sums of Enrich Remember.s
8 Videos
- INTRODUCTION TO EUCLID.S GEOMETRYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - INTRODUCTION TO EUCLID.S GEOMETRYEXERCISE - MULTIPLE CHOICE QUESTIONS
3 Videos
- PROBABILITY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - Multiple Choice Questions (MCQs)
10 Videos
Similar Questions
Knowledge Check

In the above figure , DEF is a triangle whose side DF is produced to G .HF and HD are the bisectors of ∠EFGand∠EDG , respectively . If ∠DEF=231(2)∘ , then ∠DHF (in degrees) = _______.A1112B1125C1134D1113In the given figure AB||CDandEF||DQ. Find the value of ∠DEF:
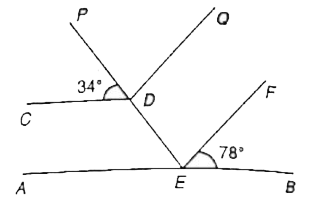 A68∘B78∘C34∘D39∘
A68∘B78∘C34∘D39∘
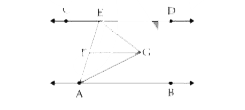
If AB||CD, EG is angle bisector of ∠DEF, FG = 12 EA and F is mid point of AE. ∠DEG=55∘, then find the value of ∠GAB?
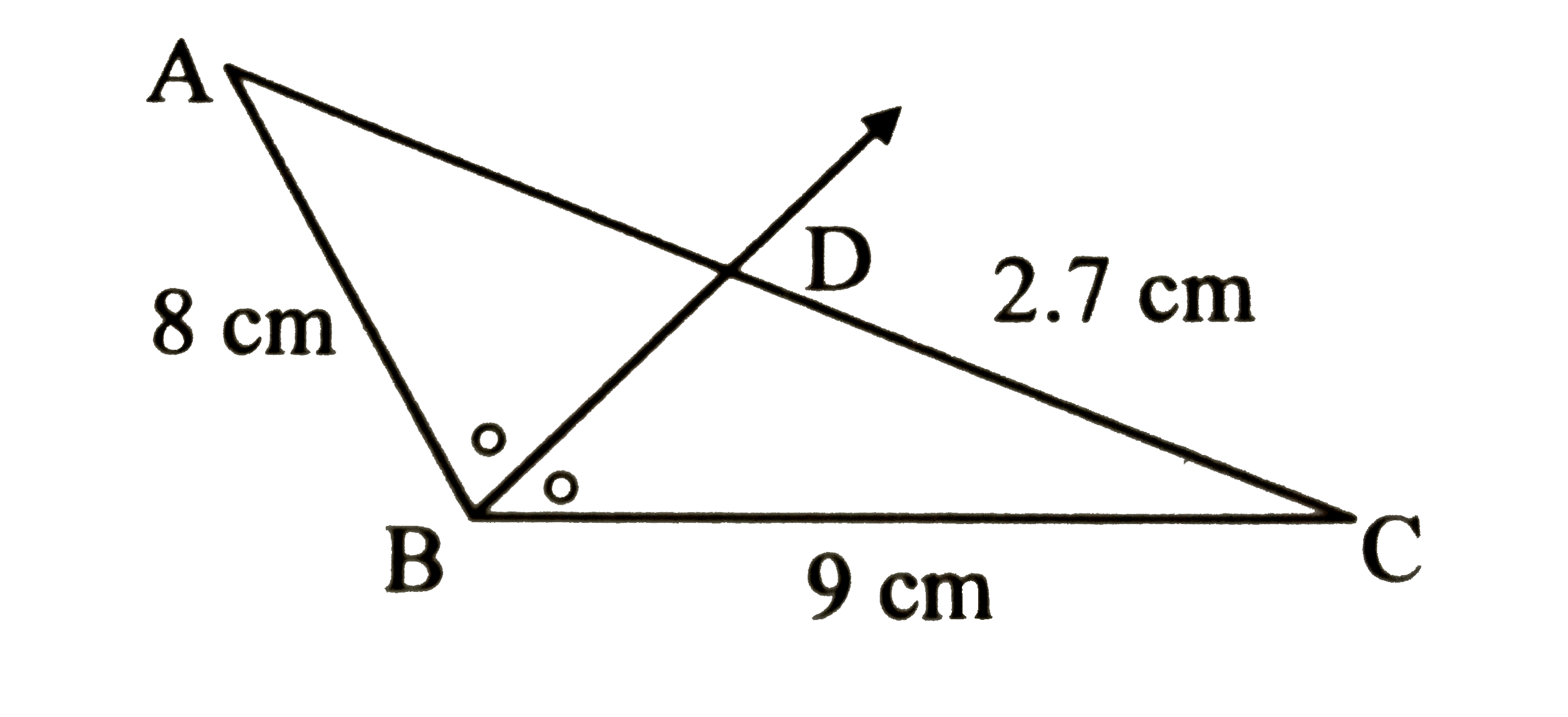
View SolutionRay BD is the angle bisector of ∠ABC. The perimeter of ΔABC is
View Solution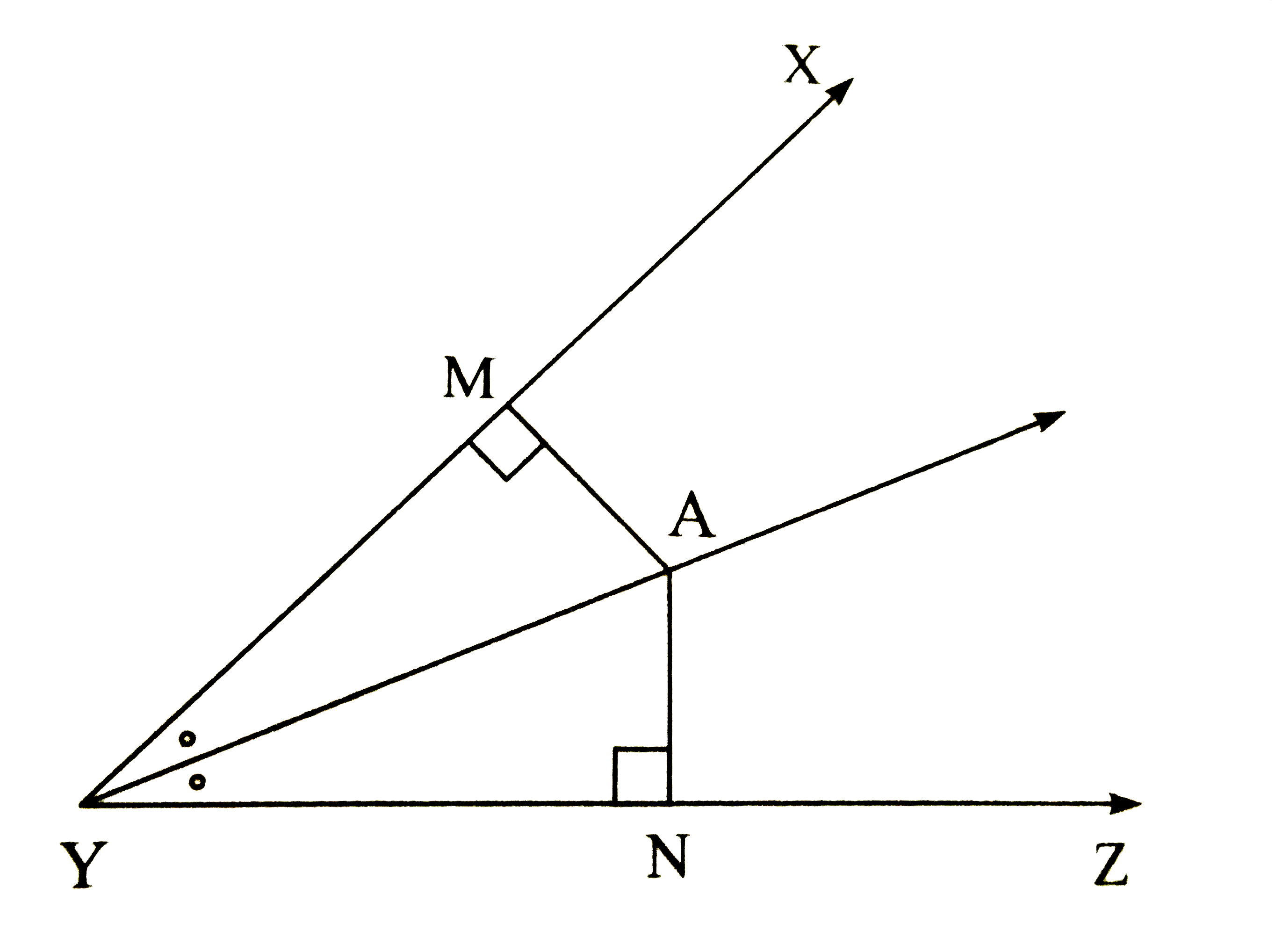
In the figure , ray YA is the bisector of ∠ XYZ if AM =2 cm then find AN. Justify .
View Solution
In the given figure, ray PT is the bisector of ∠QPR.
Find the value of x.

View SolutionIn the figure if EC is the bisector of ∠BCDandAB||CD||EF. Find ∠ABC
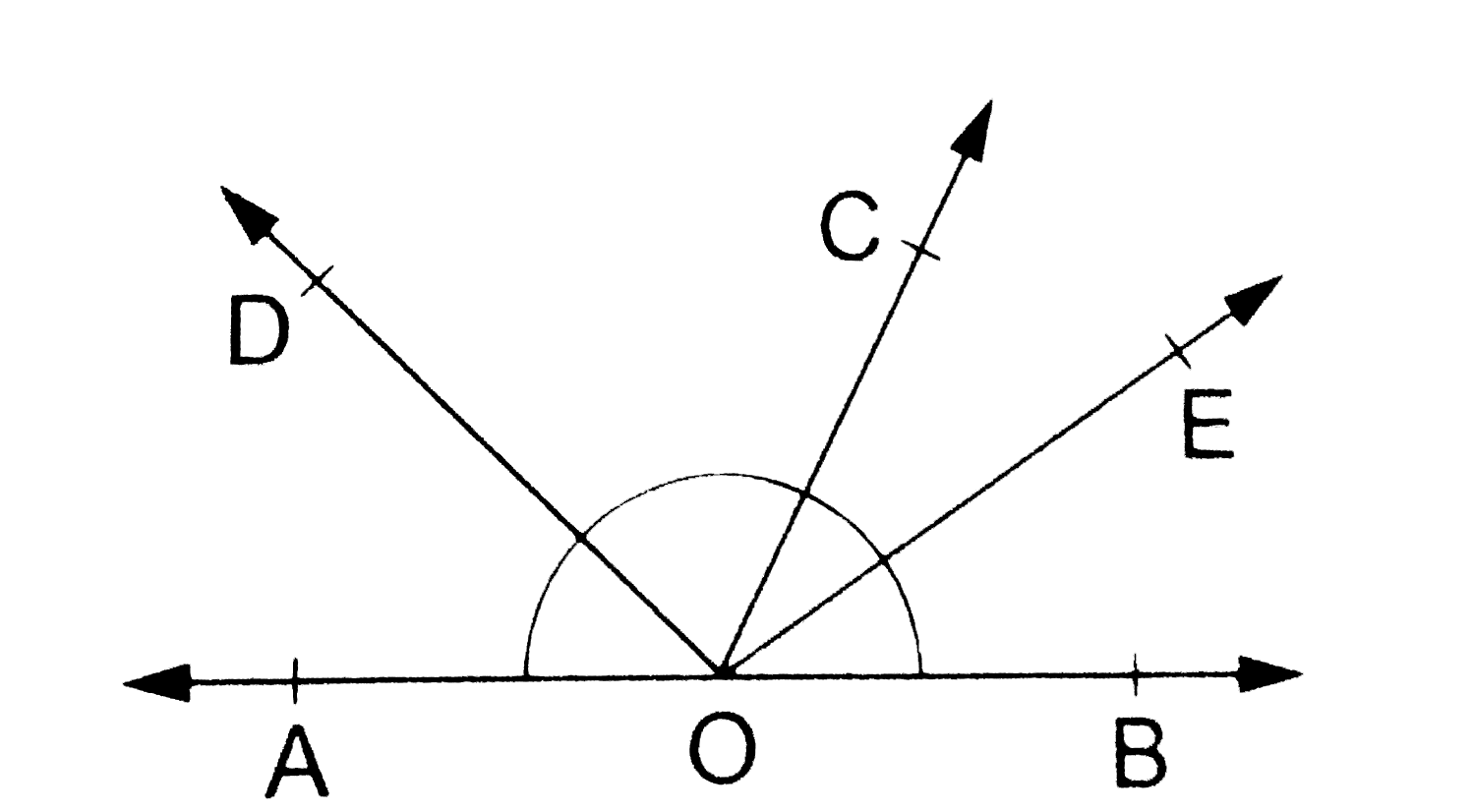
View SolutionIn the given figure, ray OC stands on a straight line AOB. Ray OD and ray OE are the bisectors of ∠AOC and ∠BOC respectively. Find the measure of ∠DOE.
View Solution

