A tyre manufacturing company kept a record of the distance covered before a tyre needed to be replaced . The table shows the results of 1000 cases :
Distance (in km)less than 40004000 to 90009001 to 14000more than 14000Frequency20210325445
If you buy a tyre of this company , what is the probability that :
it will need to be replaced before it has covered 4000 km ?
The correct Answer is:0.02
To solve the problem, we need to find the probability that a tyre will need to be replaced before it has covered 4000 km.
1. Identify the Favourable Outcomes:
The problem states that we are interested in tyres that need to be replaced before they have covered 4000 km. According to the given data, the frequency of tyres that fall into this category is 20.
2. Identify the Total Outcomes:
To find the total number of tyres recorded, we need to sum the frequencies of all categories:
- Less than 4000 km: 20
- 4000 to 9000 km: 210
- 9001 to 14000 km: 325
- More than 14000 km: 445
Total = 20 + 210 + 325 + 445 = 1000
3. Calculate the Probability:
The probability P that a tyre will need to be replaced before it has covered 4000 km is given by the formula:
P(less than 4000 km)=Number of Favourable OutcomesTotal Number of Outcomes
Substituting the values we have:
P(less than 4000 km)=201000
4. Simplify the Probability:
Now, we simplify the fraction:
P(less than 4000 km)=201000=0.02
5. Final Answer:
Therefore, the probability that a tyre will need to be replaced before it has covered 4000 km is 0.02.
The problem states that we are interested in tyres that need to be replaced before they have covered 4000 km. According to the given data, the frequency of tyres that fall into this category is 20.
To find the total number of tyres recorded, we need to sum the frequencies of all categories:
- Less than 4000 km: 20
- 4000 to 9000 km: 210
- 9001 to 14000 km: 325
- More than 14000 km: 445
The probability P that a tyre will need to be replaced before it has covered 4000 km is given by the formula:
P(less than 4000 km)=Number of Favourable OutcomesTotal Number of Outcomes
Substituting the values we have:
P(less than 4000 km)=201000
Now, we simplify the fraction:
P(less than 4000 km)=201000=0.02
Therefore, the probability that a tyre will need to be replaced before it has covered 4000 km is 0.02.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - Skill Testing Exercise8videos
PROBABILITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - EXERCISE 15.123videos
PROBABILITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINE AND ANGLESEXERCISE - Multiple Choice Questions MCQs)10videos
LINE AND ANGLES
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS18videos
SURFACE AREAS AND VOLUMES
Similar Questions
A tyre manufacturing company kept a record of the distance covered before a tyre needed to be replaced . The table shows the results of 1000 cases :
Distance (in km)less than 40004000 to 90009001 to 14000more than 14000Frequency20210325445
If you buy a tyre of this company , what is the probability that :
it will need to be replaced after it has covered somewhere between 4000 km and 14000 km ?View SolutionA tyre manufacturing company kept a record of the distance covered before a tyre needed to be replaced . The table shows the results of 1000 cases :
Distance (in km)less than 40004000 to 90009001 to 14000more than 14000Frequency20210325445
If you buy a tyre of this company , what is the probability that :
it will last more than 9000 km ?View Solution
Knowledge Check
- Question 1 - Select One
The pesticides need to be replaced because these
Aare very costlyBcannot be stored for a long timeCare mostly toxic and non-biodegradableDcause abnormalities in the target population. - Question 2 - Select One
Tyres are grooved to
ADecrease frictionBIncrease frictionCIncrease weightDDecrease the weight
A tyre manufacturing company kept a record of the distance covered before a tyre to be replaced. Following table shows the results of 1000 cases. Distance in km: Less tan 400 400 to 900 900 to 1400 More than 1400 Number of tyres: 210 325 385 80 If you boy a tyre of this company, what is the probability that: (i) it will need to be replaced before it has covered 400 km? (ii) it will last more than 900 km? (iii) it will need to be replaced after it has covered somewhere between 400 km and 1400 km? (iv) it will not need to be replaced at all? (v) it will need to be replaced?
View SolutionA tyre manufacturing company kept a record of the distance covered before a tyre to be replaced. Following table shows the results of 1000 cases. Distance ∈ km: Less than 400 400 → 900 900 → 1400 More than 1400 N⊙ of tyres: 210 325 385 80 If you buy a tyre of this company, what is the probability that: it will need to be replaced before it has covered 400 km? it will last more than 900 km? it will need to be replaced after it has covered somewhere between 400km and 1400 km? it will not need to be replaced at all it will need to be replaced?
View SolutionA tyre manufacturing company kept a record of the distance covered before a tyre needed to be placed . The table given below shows the results of 1000 cases .
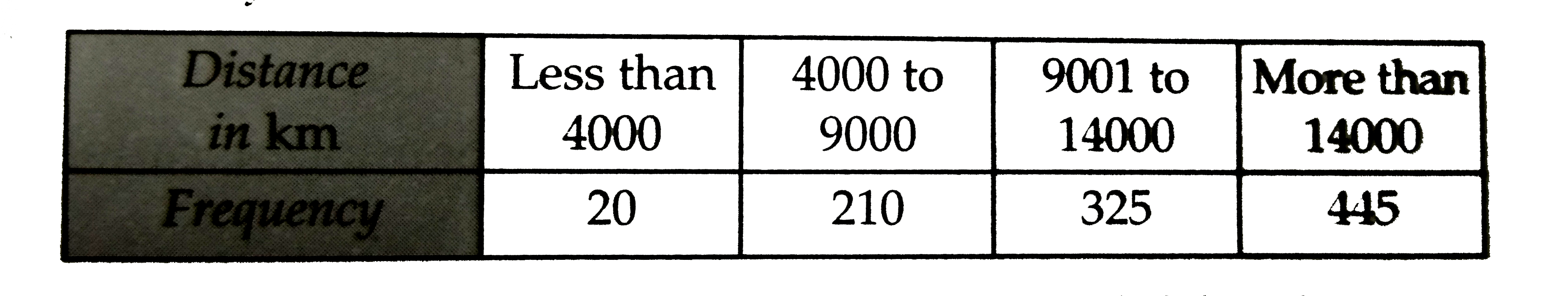
If you buy a tyre of this company , what is the probability that
(i) it will need to be replaced before it has covered 4000 km ?
(ii) It will last more than 9000 km ?
(iii) it will need to be replaced after it has covered somewhere between 4000 km and 14000 km ?View SolutionA bulb-manufacturing company kept a record of the number of hours it can glow before a bulb needed to be replaced. The following table shows the results of 500 bulbs:

If you buy a bulb of this company, then find the probability of the following events:
(a) The bulb needs to be replaced before it glows for less than 1500 hours.
(b) The bulb needs to be replaced when it glows between 1500 hours and 5000 hours.
(c) The bulb lasts for more than 2500 hours.View SolutionRubber tyres are perferred to steel tyres . Why ?
View SolutionDeep grooves in the tyres of a tractor :
View Solution

