Consider a pendulum consisting of a nuscless string with a mass on the end. The mass is held with the string horizontal, and then released. The mass swings down, and on its way back up, the string is cut at point P when it makes an angle of $θ$ with the vertical. Find $θ$ if that mass covers maximum horizontal range.

Text Solution

Verified by Experts

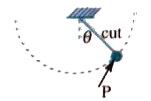
The speed at angle $θ$ is given by conservation of energy.
$\frac{1}{2} m v^{2} = m g h \Rightarrow \frac{1}{2} m v^{2} = m g R cos θ v = \sqrt{2 g R cos θ}$
When string is cut particle moves as a projectile with velocity component.
$v_{x} = v cos θ v_{y} = v sin θ$
The time of flight is $t = 2 (\frac{v_{y}}{g})$
Range is, $x = v_{x} t = v_{x} (\frac{2 v_{y}}{g})$
$= \frac{2 v_{x} v_{y}}{g} = \frac{2 (v cos θ) (v sin θ)}{g}$
$= \frac{2 v^{2} sin θ cos θ}{g} = \frac{2 (2 g R cos θ) sin θ cos θ}{g} = 4 R {cos}^{2} θ sin θ$
Take the derivative of this function and equate it to zero
Thus we get $0 = 4 R [(- 2 cos θ sin θ) sin θ + {cos}^{2} θ cos θ]$ (or)
$2 {sin}^{2} θ cos θ = {cos}^{3} θ (or) tan θ = 1 / \sqrt{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Similar Questions

Knowledge Check

Question 1 - Select One
In a simple pendulum, the breaking strength of the string is double the weight of the bob. The bob is released from rest when the string is horizontal. The string breaks when it makes an angle $θ$ with the vertical.
A $θ = {cos}^{- 1} (1 / 3)$
B $θ = 60^{\circ}$
C $θ = {cos}^{- 1} (2 / 3)$
D $θ = 0$
Question 2 - Select One
A simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle $θ$ with the vertical. The angle $θ$ is equal to
A $\frac{π}{4}$
B ${cos}^{- 1} (\frac{1}{\sqrt{3}})$
C ${sin}^{- 1} (\frac{1}{\sqrt{3}})$
D $\frac{π}{3}$
Question 3 - Select One
A simple pendulum of length L swings in a vertical plane. The tension of the string when it makes an angle $θ$ with the vertical and the bob of mass m moves with a speed v is (g is the gravitational acceleration)
A $m v^{2} / L$
B $m g cos θ + m v^{2} / L$
C $m g cos θ - m v^{2} / L$
D $m g cos θ$

Recommended Questions

Home
Ask Doubt
Profile