A block of mass m and a pan of equal mass are connected by a string going over a smooth light pulley. Initially the system is at rest when a particle of mass m falls on the pan and sticks to it. If the particle strikes the pan with a speed v, find the speed with which the system moves just after the collision.
Let the required speed be V. , Further, let
J1= imulse between particle and pan,
J2= impulse imparted to the block and the pan by the string.
Using impulse = change in momentum.
For paticle, J1=mv−mV….(1),
For pan,J1−J2=mV....(2),
For block,J2=mV....(3)
Solving these three equations, we get V=v3
Topper's Solved these Questions
- COLLISIONS BOOK - AAKASH SERIESCHAPTER - COLLISIONS EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
12 Videos
- COLLISIONS BOOK - AAKASH SERIESCHAPTER - COLLISIONS EXERCISE - NUMERICAL EXERCISE ( LEVEL 1)
18 Videos
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED))
3 Videos
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - Questions for Descriptive Answers
10 Videos
Similar Questions
A block of mass m and a pan of equal mass are connected by a string going over a smooth light pulley as shown in figure. Initially the system is at rest when a particle of mass m falls on the pan and sticks to it. If the particle strikes the pan with a speed v find the speed with which the system moves just after the collision.
View SolutionA block of mass m and α pan of equla mass are connected by a string going over a smooth light pulley as shwon in figure. Initially the systemis at rest when a particle of mass m falls on the pan and sticks to it. If the particle strikes thepan witha speed v find the speed with which the system moves just after the collision.
View Solution
Knowledge Check
Two masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration
 Ag(M−mM+m) downwardBg(M−mM+m)2 downwardCg(M−mM+m)2 upward if M<mDzero
Ag(M−mM+m) downwardBg(M−mM+m)2 downwardCg(M−mM+m)2 upward if M<mDzeroA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
A0.8vB0.2vC0.6vD0.4vA particle of mass m moving with velocity v strikes a stationary particle of mass 2m and sticks to it. The speed of the system will be.
Av//2B2 vCv//3D3 v
Two masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration

View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it. The speed of the system will be
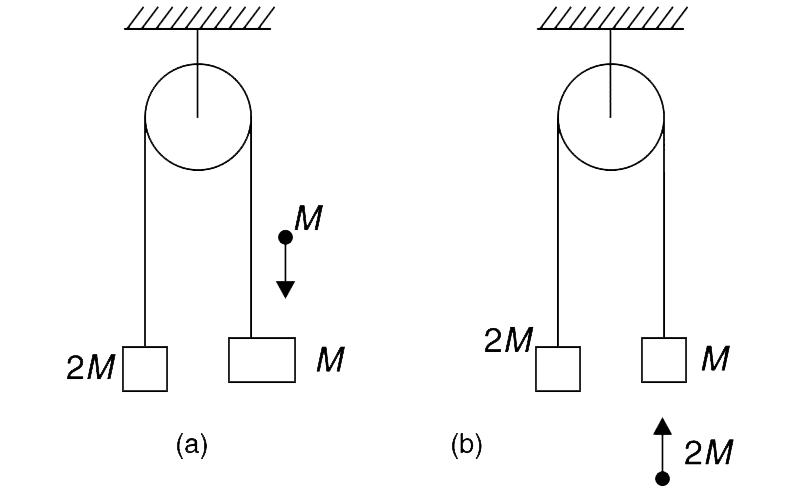
View SolutionTwo blocks of mass M and 2M are connected to the two ends of a light, inextensible string passing over an ideal pulley as shown in figure. The system is released from rest.
(a) One second after the system is released, a particle of mass M hits the block of mass M and sticks to it. The particle hits the block with a speed of 10 m/s while travelling downward. Find the total distance travelled by block of mass 2M after it is released.
(b) One second after the system is released, a particle of mass 2M hits the block of mass M and sticks to it. The particle hits the block with a speed of 10 m/s while travelling in upward direction. Find distance travelled by the block of mass 2M after it is released to the time it comes to rest for the first time (g=10m/s)2
View SolutionTwo blocks of mass m1andm2 are connected by light inextensible string passing over a smooth fixed pulleuy of negligible mass. The acceleration of the centre of mass of the system when blocks move under gravity is :
View Solution
