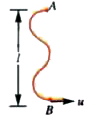
A string AB of length 21 is fixed at A to a point on a smooth horizontal table. A particle - of mass m attached to B is initially at a distance I from A as shown in figure. The particle is projected horizontally with speed u at right angles to AB. Find the impulsive tension in the string when it becomes taut and the velocity of the particle immediately afterwards.

Text Solution

Verified by Experts

When the string b eomes thut $A B . = 2 l and ∠ B . A B = 60^{\circ}$

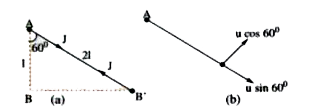
Just before the string jerks, the particles is velocity components parallel and perpendicular to AB. are u ${sin 60}^{\circ}$ and u ${cos 60}^{\circ}$ respectively. When the string becomes thut the length of AB is fixed and particle cannot travel in the direction AB.. After the jerk, the velocity of the particle is, therefore, perpendicular to AB.. Using impulse = change in momentum
(a) Along $B . A, J = 0 - (- m u {sin 60}^{\circ}) (or) J = \frac{\sqrt{3}}{2} m u$
(b) Perpendicular to B.A (no impulsive component) $0 = m v - m u {cos 60}^{\circ} (or) v = u {cos 60}^{\circ} = \frac{u}{2}$
Therefore, the velocity of the particle just after the string becomes thut is $\frac{u}{2}$ perpendicular to the string.

Updated on:21/07/2023

A stone hanging from a massless string of length 15m is projected horizontally with speed $\sqrt{147} m s^{- 1}$ Then the Speed of the particle, at the point where tension in string equals the weight of particle, is
A $10 m s^{- 1}$
B $7 m s^{- 1}$
C $12 m s^{- 1}$
Dnone of these
A stone hanging from a massless string of length 15m is projected horizontally with speed $\sqrt{147} m s^{- 1}$ Then the Speed of the particle, at the point where tension in string equals the weight of particle, is
A $10 m s^{- 1}$
B $7 m s^{- 1}$
C $12 m s^{- 1}$
Dnone of these