Two blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks pulling it away from the other as shown in figure, (a) Find the displacement of the centre of mass at time t. (b) If the extension of the spring is x0 at time t, find the displacement of the two blocks at this instant:

(a) The acceleration of the centre of mass is aCM=F2m
The displacement of the centre of mass at time t will be x=12aCM.t2=Ft24m
(b) Suppose the displacement of the first block is x1 and that of the second is x2. Then,
x=mx1+mx22m or Ft24m=x1+x22 (or) x1+x2=Ft22m.........(i)
Further, the extension of the spring is x1−x2
Therefore, x1−x2=x0............(ii)
From Eqs. (i) and (ii), x1=12(Ft22m+x0) and x2=12(Ft22m−x0)
Similar Questions
Two block of equal mass m are connected by an unstretched spring and the sytem is kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks puling it away from the other as shown in figure. a.Find the positon of the centre of mass at time t. b.If the extansion of the spring is x0 at time t find the displacement of the two blocks at this instant.
View SolutionTwo block of equal mass m are connected by an unstretched spring and the sytem is kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks puling it away from the other as shown in figure. a.Find the positon of the centre of mass at time t. b.If the extansion of the spring is x0 at time t find the displacement of the two blocks at this instant.
View Solution
Knowledge Check
Two blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

Then the displacement of the centre of mass in at time t isAFt22mBFt23mCFt24mDFt2mTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is x0 at time t, then the displacement of the second block at this instant isAFt22m−x0B12(Ft22m+x0)C12(2F2m−x0)D12(Ft22m−x0)Two blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is x0 at time t, then the displacement of the first block at this instant isA12(Ft22m+x0)B−12(Ft22m+x0)C12(Ft22m−x0)DFt22m+x0
Two blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

Then the displacement of the centre of mass in at time t is
View Solutiontwo blocks of equal mass m are connected by an unstretched· spring and the system is kept at rest on a frictionless horizontal surface. A constant force Fis applied on one of the blocks pulling it away from the other as shown in Fig. ,4E.21(a)
(a) find tyhe position of CM at time t,
(b) if the extension of the spring is x0 at time t, find the displacement of the blocks at that instant.
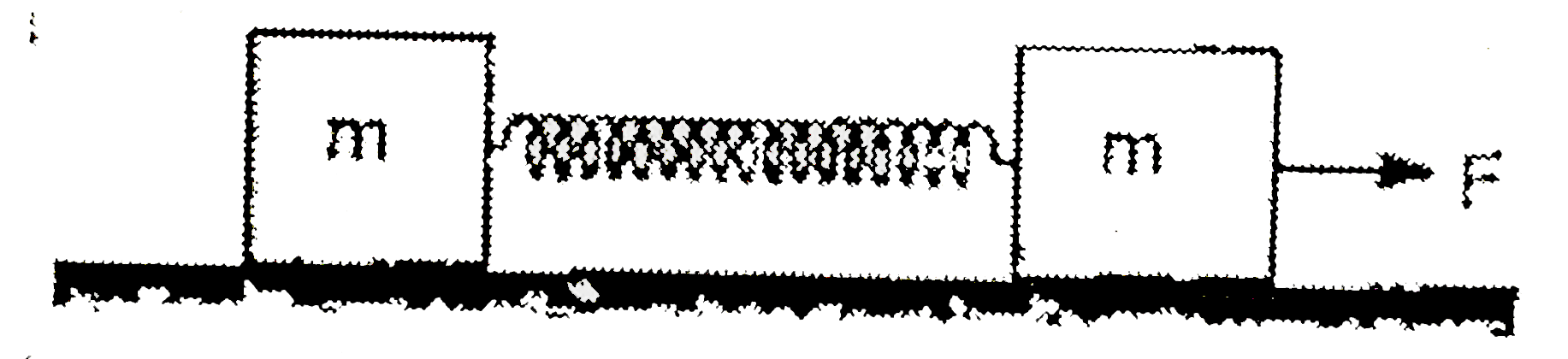
View SolutionTwo blocks each of mass m, connected by an un-stretched spring are kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks pulling it away from the other as shown in figure.
(a)Find accelaration of the mass center.
(b) Find the displacement of the centre of mass as function of time t.
(c) If the extension of the spring is X0 at an instant t, find the displacements of the two blocks relative to the ground at this instant.
View SolutionTwo blocks each of mass m, connected by an un-stretched spring are kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks pulling it away from the other as shown in figure.
 (a)Find accelaration of the mass center.
(a)Find accelaration of the mass center.
(b) Find the displacement of the centre of mass as function of time t.
(c) If the extension of the spring is X0 at an instant t, find the displacements of the two blocks relative to the ground at this instant.
View SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is x0 at time t, then the displacement of the first block at this instant is
View Solution
