A load of 31.4 kg is suspended from a wire of radius 10−3m and density 9×103kg/m3. Calculate the change in temperature of the wire if 75% of the work done is converted into heat. The Young.s modulus and heat capacity of the material of the wire are 9.8x1010N/m2 and 490 J/kg K respectively.
As work done in stretching an elastic body per unit volume is given by
WV=12stress×strain=12stressY[asY=stressstrain]
SoW=12[MgA]2VY[as stress=FA=MgA]
Now according to given Problem H=(75/100)W
msΔθ=34×12Mgπr2]VY(or)(ρV)sΔθ=34×12[mgπ2]2VY
∴Δθ=38[31.4×9.8π×10−6]219.8×1010×19×103×490
i.e,Δθ=1120K=8.33×10−3K
Topper's Solved these Questions
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - TEST YOUR SELF
11 Videos
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - Very Short Answer Type Questions
15 Videos
- COLLISIONS BOOK - AAKASH SERIESCHAPTER - COLLISIONS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
4 Videos
- ELEMENTS OF VECTORS BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWER
10 Videos
Similar Questions
A load of 31.4 kg is suspended from a wire of radius 10−3 m and density 9×103kg/m3 Calculate the change is temperature of the wire if 75% of the work done is converted into heat. The Young's modulus and the specific heat capactiy of the meterial of the wire are 9.8×1010N/m2and490J/kg/K respectively.
View SolutionA load of 40 kg is suspended from a wire of radius 10−3m and density 8×10kgm−375% of the work done to increase the length is converted into heat. Calculate the change in temperature (in kelvin) of the wire . Given that Y=7.5×1010Nm−2 and heat capacity of the material of the wire is 490JkgK−1 respectively. (Take π2=9.8andg=9.8m/s2)
View Solution
Knowledge Check
A load of 3kg produces an extension of 1.5mm in a wire of length 3m and diameter 2mm. Young's modulus of the material of the wire is
A1.87×1010Nm−2B3.5×1010Nm−2C15×1010Nm−2D2.5×1010Nm−2The density of a uniform steel wire of mass 1.6×10−2kg, and length 2.5 m is 8×103kg/m3. When it is loaded by 8kg, it elongates by 1.25 mm. If g=10m/s2, then the Young's modulus of the material of the wire is
A1.5×1011N/m2B2×1011N/m2C1.75×1011N/m2D1.5×1012N/m2
(a) A wire 4m long and 0.3 mm, calculate the potential energy stored in the wire.
Young's modulus for the material of wire is 2.0×1011N/m2.
View Solution(a) A wire 4m long and 0.3 mm, calculate the potential energy stored in the wire.
Young's modulus for the material of wire is 2.0×1011N/m2.
View SolutionA 10 kg mass is attached to one end of a copper wire, 3m long and 1 mm in diameter. Calculate the lateral compression produced in it. (Possion's ration is 0.25and Young's modulus, of the metereal of the wire is modulus of the material of the wire is 12.5×1010N/m2).
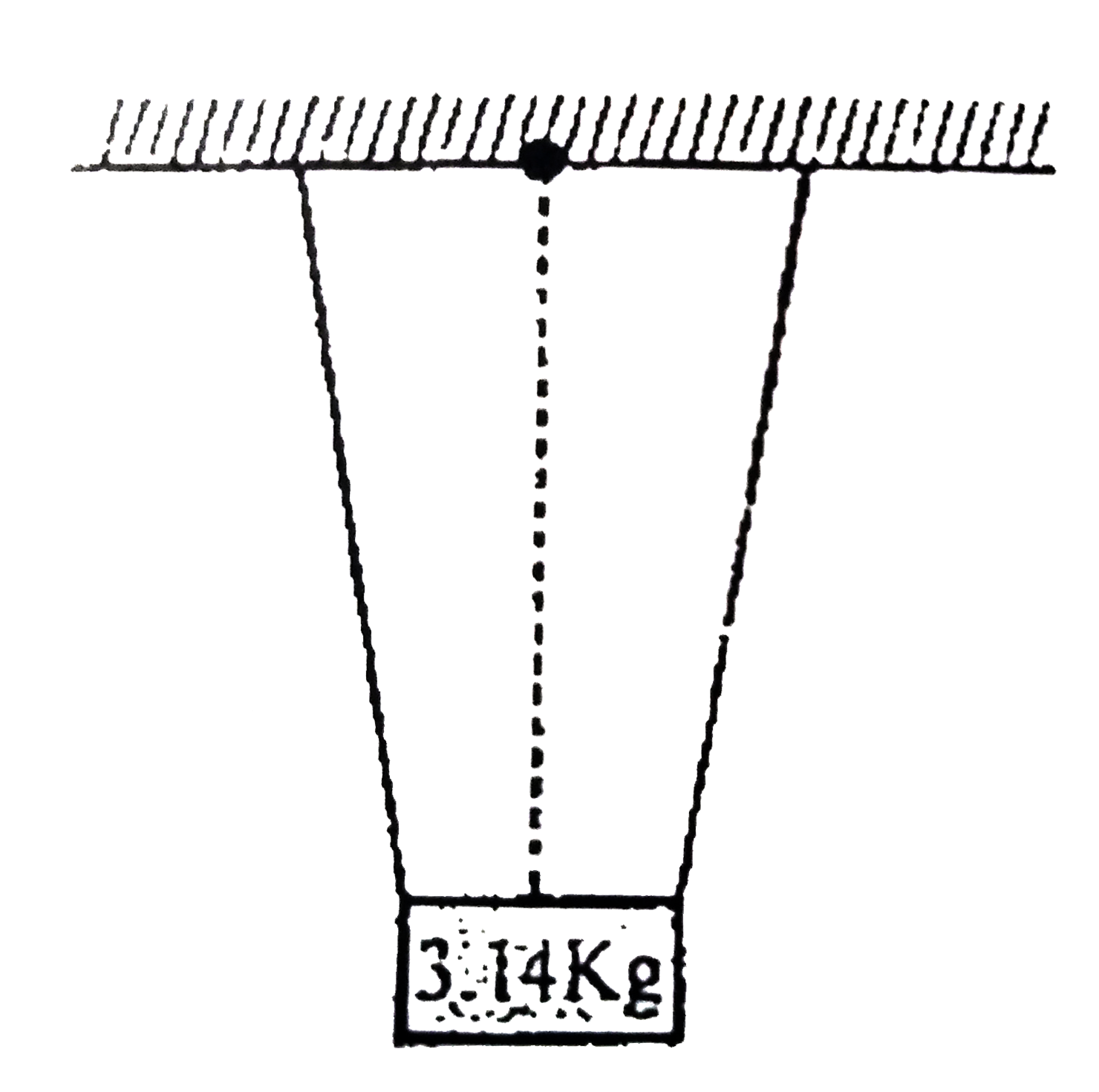
View SolutionA body of mass 3.14 kg is suspended from one end of a non uniform wire of length 10m, such that the radius of the wire is changing uniformly from 9.8×10−4 m at one end to 5×10−4 m at the other end. Find the change in length of the wire in mm. Young's modulus of the material of the wire is 2×1011N/m2 (mass of wire is negligible)
View SolutionCalculate the speed of a transverse wave in a wire of 1.0mm2 cross-section under a tension of 0.98N. Density of the material of wire is 9.8×103kg/m3
View SolutionCalculate the speed of a transverse wave in a wire of 1.0mm2 cross-section under a tension of 0.98N. Density of the material of wire is 9.8×103kg/m3
View Solution
