A planet revolves around sun in an elliptical orbit of eccentricity .e.. If .T. is the time period of the planet then show that the time spent by the planet between the end of the minor axis and close to sun is T(14−e2π)
dAdt=constant ,

tABT=(Area) SAB(Area) ellipse=πab4−12b(ea)πab
Topper's Solved these Questions
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - Exercise-I
124 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - Exercise-II
78 Videos
- GAUSS.S LAW BOOK - AAKASH SERIESCHAPTER - GAUSS.S LAW EXERCISE - PROBLEMS (LEVEL - II)
12 Videos
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -3
154 Videos
Similar Questions
A planet is revolving around the sun in an elliptical orbit having eccentricity e(=π4). If the time period of revolution is 16 months then find the time taken by the planet in going from A to B in months.
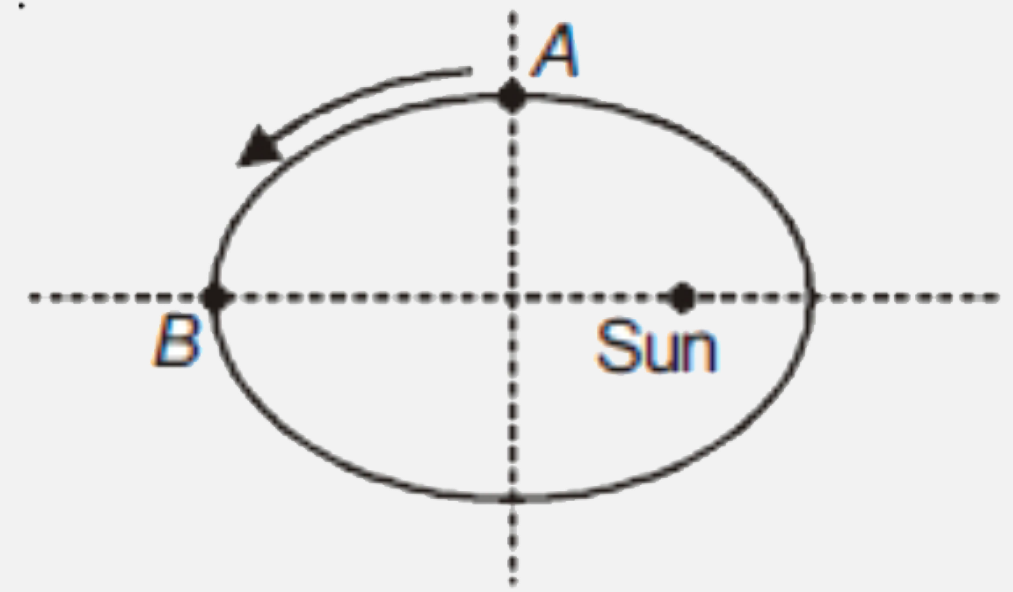
View SolutionA planet revolves around the sun in an elliptical . The linear speed of the planet will be maximum at

View Solution
Knowledge Check
A planet revolves around the sun in elliptical orbit of eccentricity 'e'. If 'T' is the time period of the planet then the time spent by the planet between the end of the minor axis and close to the sun is
AT(14−e2π)BTeπC(eπ−1)DπTeA planet revolves around the sun in elliptical orbit of eccentricity 'e'. If 'T' is the time period of the planet then the time spent by the planet between the ends of the minor axis and major axis close to the sun is
ATπ2eBT(2eπ−1)CTe2πDT(14−e2π)A planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
A|v×r|B2|r×v|C∣∣∣12(r×v)∣∣∣DNone of these
A planet revolves around the sun in an elliptical . The linear speed of the planet will be maximum at

View SolutionA planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
View SolutionA planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at

View SolutionIf a planet of mass m is revolving around the sun in a circular orbit of radius r with time period, T then mass of the sun is
View SolutionA planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at

View Solution
