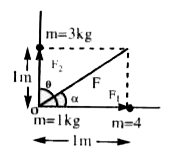
Two objects of masses 4kg and 3kg are placed along X and Y axes respectively at a distance of 1m from the origin. An object of mass 1kg is kept at the origin of the co-ordinate system. Calculate the resultant gravitational force attraction on the object at the origin.Solution in Telugu
Force due to 4kg mass on 1 kg mass at the origin is
F1=G×4×112=4G
Force due to 3 kg mass on 1kg mass at the origin is
F2=G×3×112=3G
The resultant force is found by using parallelogram
law of vectors F=√F21+F22+2F1F2cosθ
=√(4G)2+(3G)2+2(4G)(3G)cos90∘= 5G
Topper's Solved these Questions
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - Exercise-I
124 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - Exercise-II
78 Videos
- GAUSS.S LAW BOOK - AAKASH SERIESCHAPTER - GAUSS.S LAW EXERCISE - PROBLEMS (LEVEL - II)
12 Videos
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -3
154 Videos
Similar Questions
According to Kepler, the period of revolution of a planet (T) and its mean distance from the Sun (R) are related by the equation
View SolutionA planet revolves round the sun in an elliptical orbit of minor and major axes x and y respectively . Then the time period of revolution is proportional to
View SolutionA charge q is placed at the centre of the open end of a cyclindrical vessel. Find the flux of the electric through the surface of the vessel.
View SolutionA satellite takes 1/8 years to move round the earth in its permissible orbit of radius R. The period when it revolves round the earth in an orbit of radius '2R' is
View SolutionAn infinite number of particles each of mass m are placed on the positive X-axis of 1m, 2m, 4m, 8m,... from the origin. Find the magnitude of the resultant gravitational force on mass m kept at the origin.
View SolutionA 3kg mass and 4kg mass are placed on X and Y axes at a distance of 1 meter from the origin and a 1kg mass is placed at the origin. Then the resultant gravitational force on 1kg mass is
View SolutionFour particles of masses 1kg ,2kg, 3kg and 4kg are placed at the corners of a square of side 2m in the x-y plane If the origin of the co-ordinate system is taken at the mass of 1kg, the (x,y) co-ordinates of the enter of mass expressed in metre are :
View SolutionTwo particles of masses 4kg and 8kg are kept at x=-2m and x=4m respectively. Then the net gravitational force acting on a third particle of mass 1kg kept at the origin is
View SolutionTwo objects of masses 4kg and 3kg are placed along X and Y axes respectively at a distance of 1m from the origin. An object of mass 1kg is kept at the origin of the co-ordinate system Calculate the resultant gravitational force attraction on the object at the origin.
View SolutionAn infinite number of particles each of mass 1kg are placed on the positive x-axis at 1m, 2m, 4m, 8m.... from the origin. The magnitude of the resultant gravitational force on 1kg mass kept at the origin is
View SolutionTwo particles of masses 4kg and 8kg are kept at x=-2m and x=4m respectively. Then the net gravitational force acting on a third particle of mass 1kg kept at the origin is
View SolutionTwo objects of masses 4kg and 3kg are placed along X and T axes respectively at a distance of 1m from the origin. An object of mass 1kg is kept at the origin of the co-ordinate system. Calculate the resultant gravitational force attraction on the object at the origin.
View SolutionAn infinite number of particles each of mass m are placed on the positive x-axis at 1m, 2m, 4m, 8m,…. from the origin. The magnitude of the resultant gravitational force on mass 'm' kept at the origin is
View SolutionAn infinite number of particles each of mass 1kg are placed on the postive x-axis at 1m, 2m, 4m, 8m… from the origin. The magnitude of the resultant gravitational force on 1kg mass kept at the origin is
View SolutionTwo objects of masses 4kg and 3kg are placed along X and T axes respectively at a distance of 1m from the origin. An object of mass 1kg is kept at the origin of the co-ordinate system. Calculate the resultant gravitational force attraction on the object at the origin.
View Solution
