Suppose, the acceleration due to gravity at the Earth.s surface is 10m/s2 and at the surface of Mars it is 4.0 m/s2. A 60 kg passenger goes from the earth to the mars in a spaceship moving with a constant velocity. Neglect all other objects in the sky. Which part of figure best represents the weight (net gravitational force) of the passenger as a function of time.
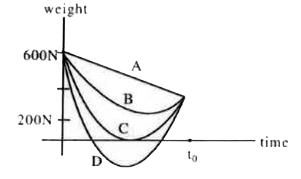
A
B
C
D
The correct Answer is:C
Topper's Solved these Questions
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - Exercise-II
78 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - Practice Exercise
56 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II) PRACTICE SHEET (ADVANCED)Integer Type Questions
6 Videos
- GAUSS.S LAW BOOK - AAKASH SERIESCHAPTER - GAUSS.S LAW EXERCISE - PROBLEMS (LEVEL - II)
12 Videos
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -3
154 Videos
Similar Questions
Suppose the acceleration due to gravity at earth's surface is 10ms−2 and at the surface of Mars it is 4.0ms−2. A passenger goes from the earth to the mars in a spaceship with a constant velocity. Neglect all other object in sky. Which part of figure best represent the weight (net gravitational force) of the passenger as a function of time?
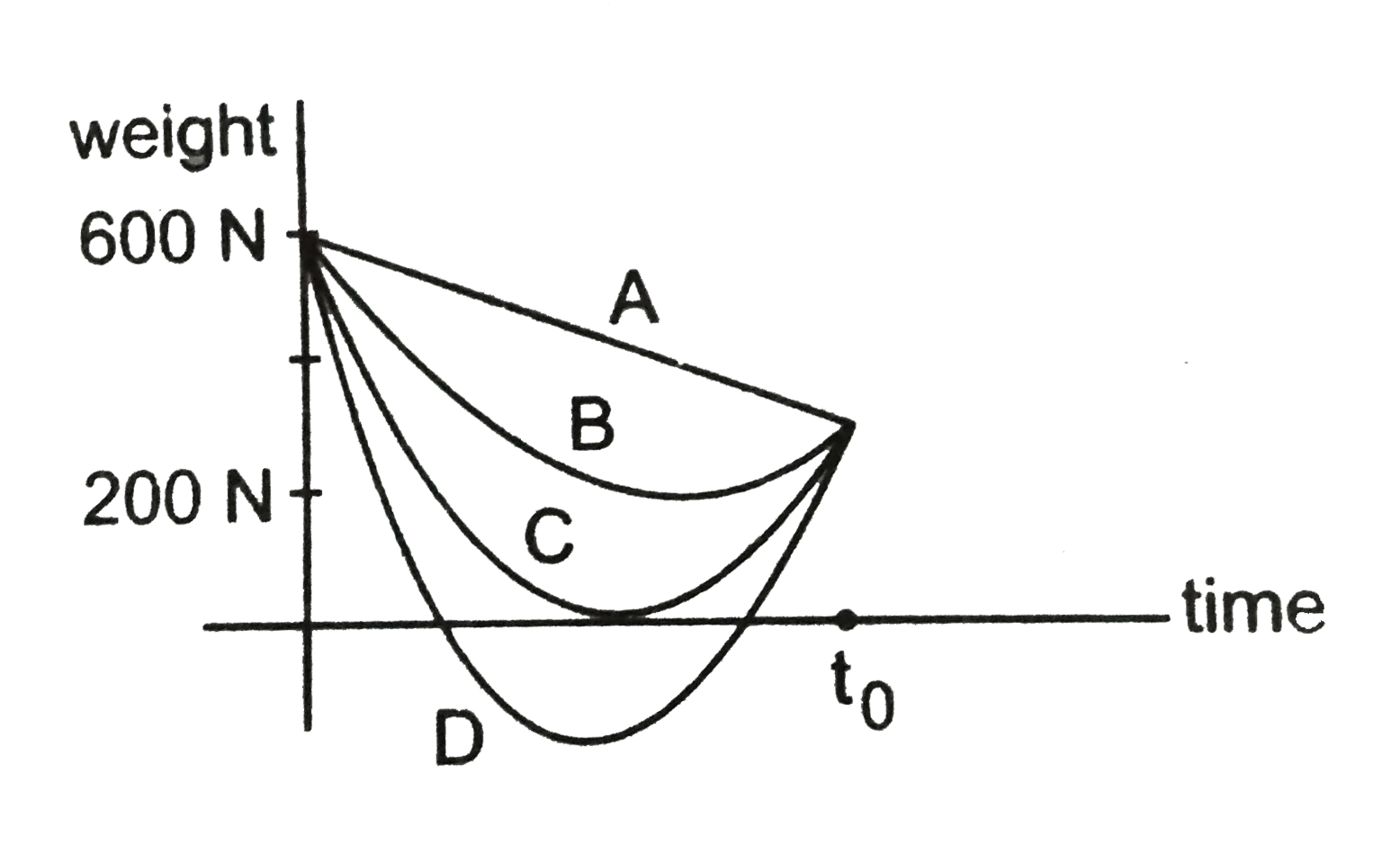
View SolutionSuppose the acceleratio due to gravity at thth's surface is 10ms−2 and at the surface of Mars it is 4.0ms−2. A passenger goes from the to the mars in a spacehip with a constant velocity. Neglect all other object in sky. Which part of figure best represent the weight (net gravitational force) of the passenger as a function of time?

View Solution
Knowledge Check
If accleration due to gravity on the surface of earth is 10ms−2 and let acceleration due to gravitational acceleration at surface of another planet of our solar system be 5ms−2 An astronaut weighing 50kg on earth goes to this planet in spaceship with a constant velcity The weight of the astronaut with time of fiight is roughly given by
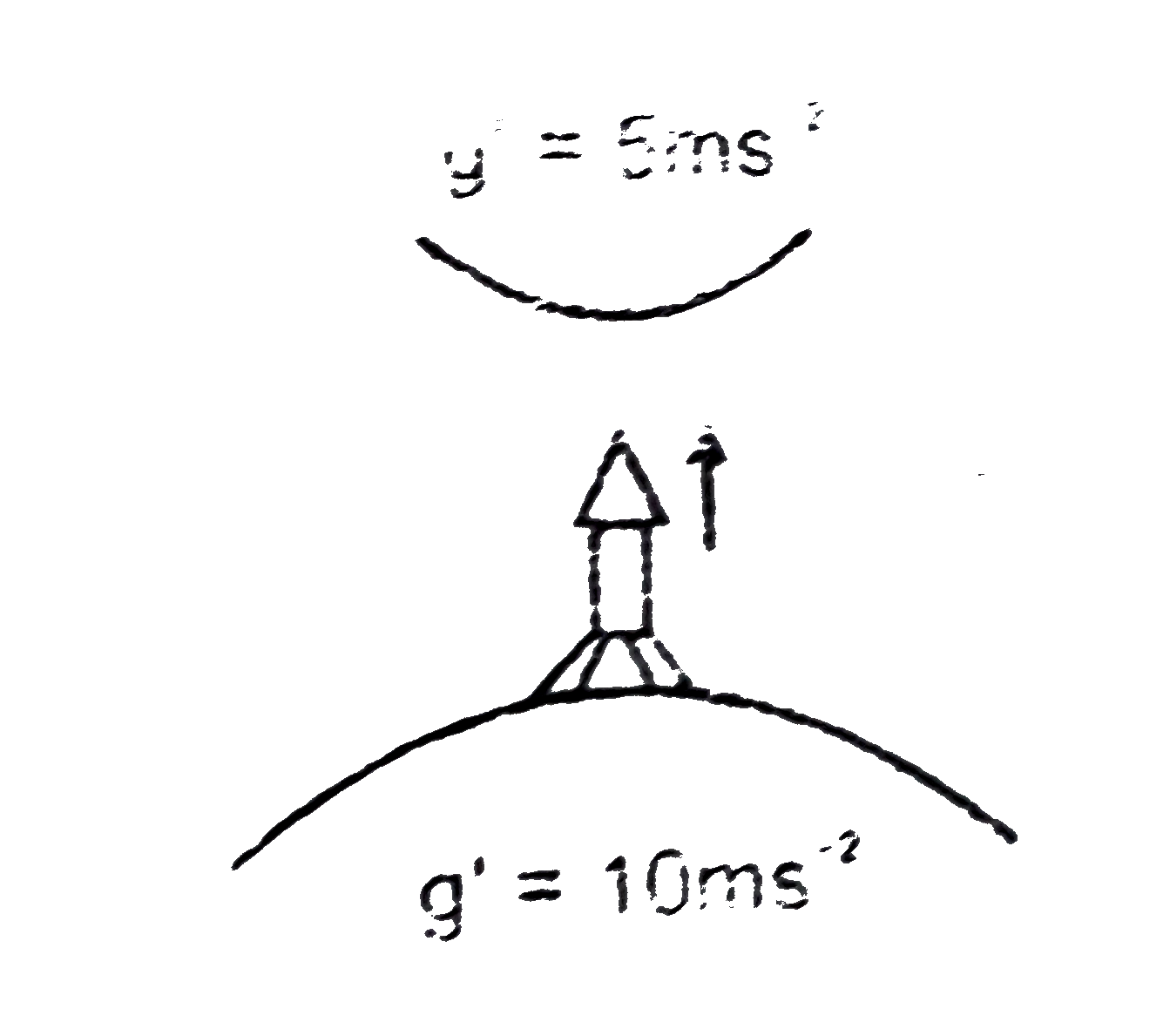 .A
.A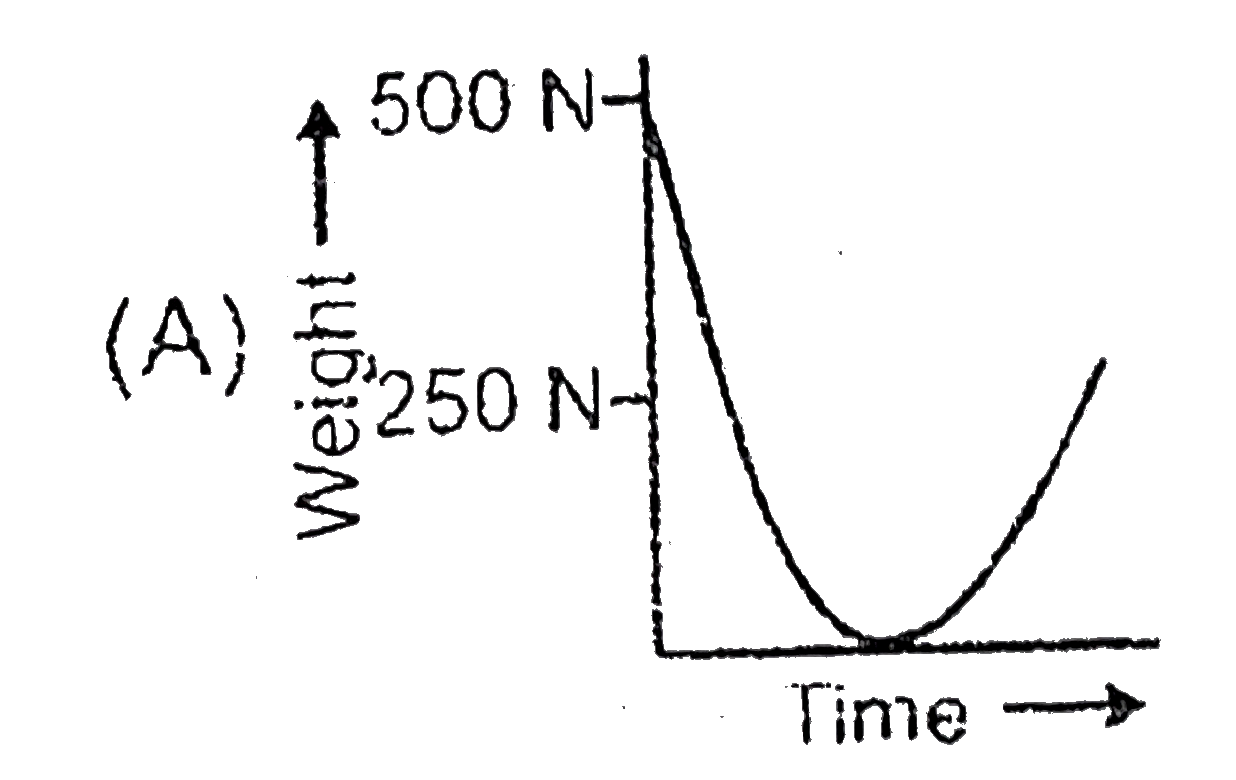 B
B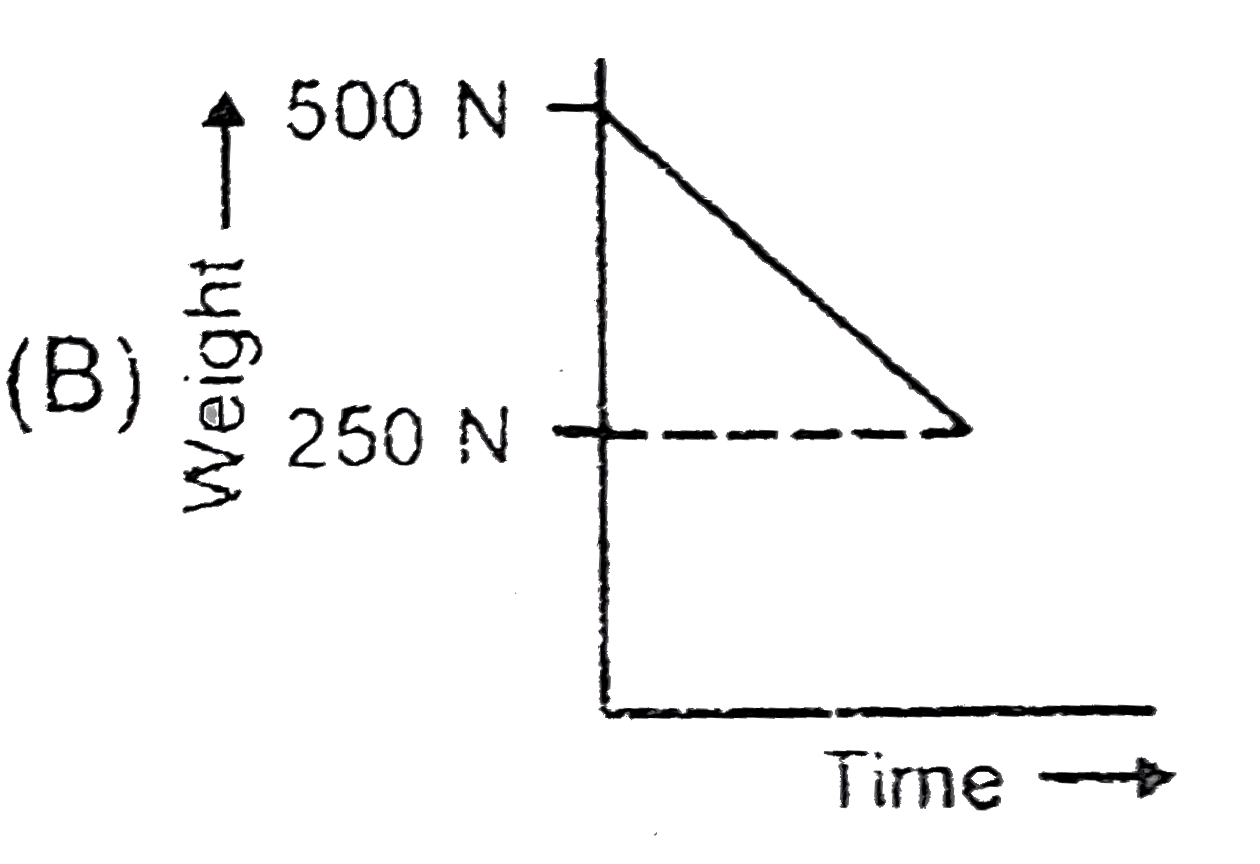 C
C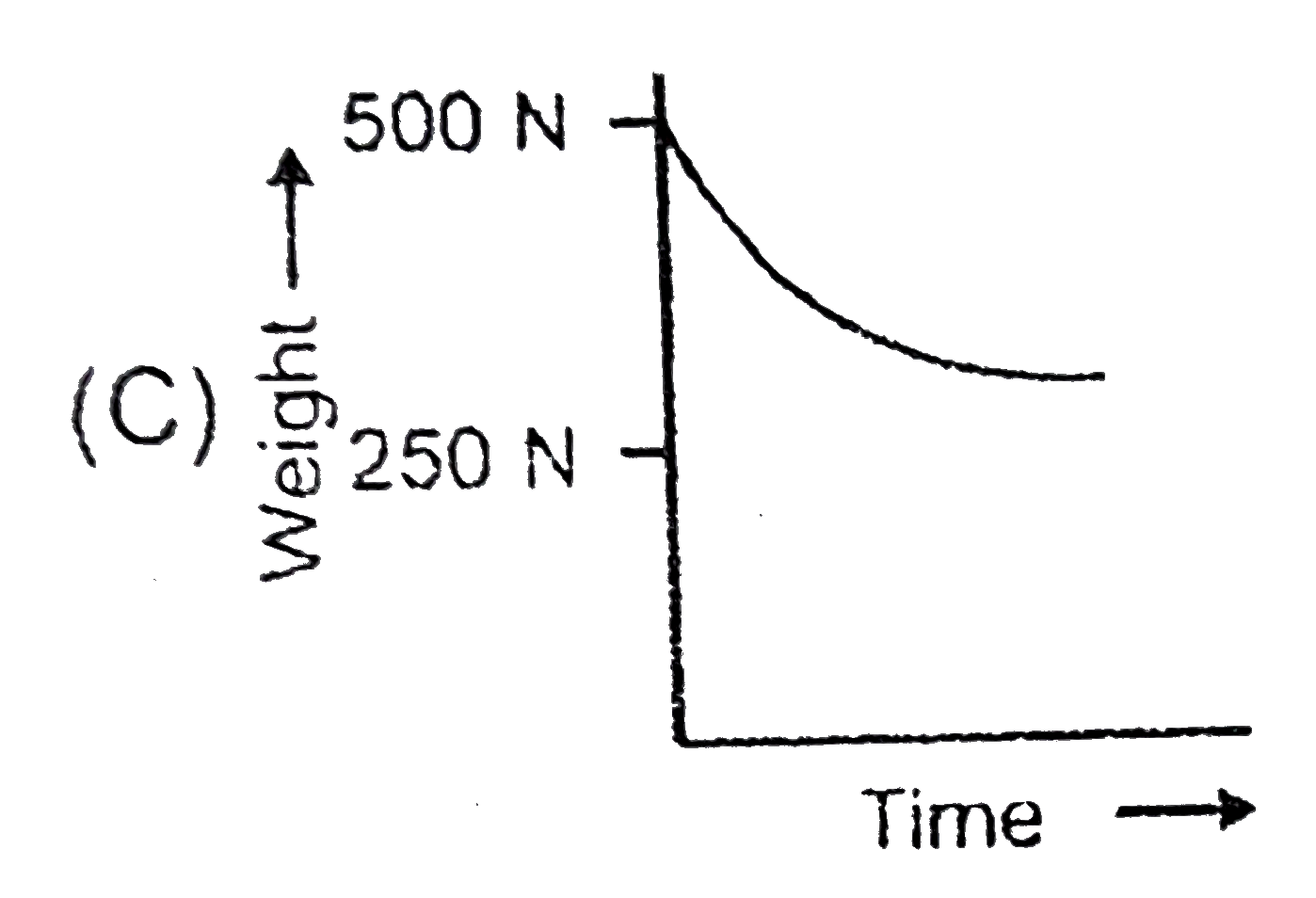 D
D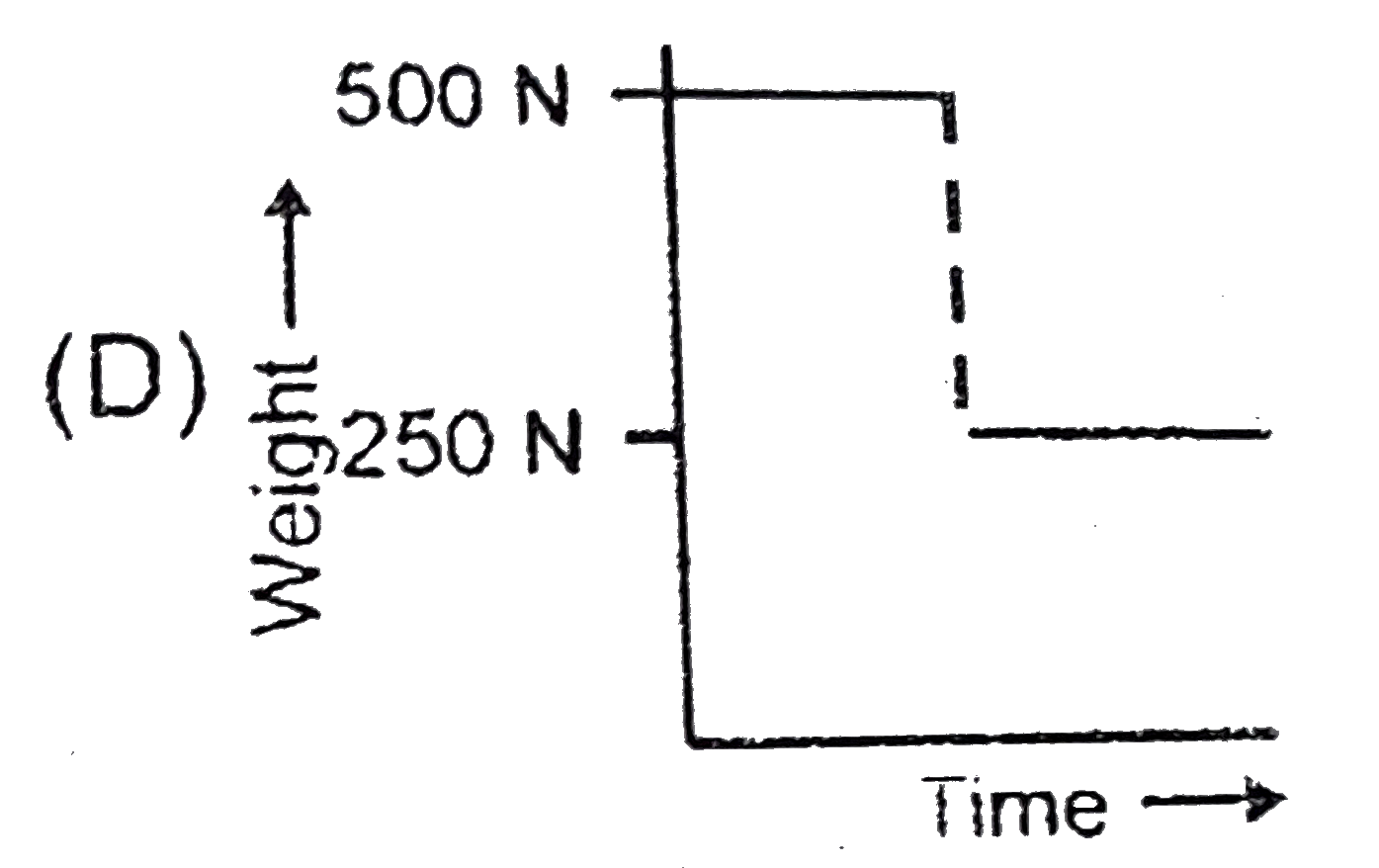
The acceleration due to gravity at a place is 0.2m/s2. Find the height above the earth's surface .
View SolutionThe acceleration due to gravity near the earth's surface is 9.8m/s2, and the earth's radius is 6,400 km.From this data calculate the mass of the earth. Use any universal constant if required.
View SolutionWhat is the acceleration due to gravity at a height h ( = radius of the earth) from the surface of the earth ? ltbgt (g=9.8m/s2)
View SolutionIf g is the acceleration due to gravity on the earth’s surface, the gain in the potential energy of an object of mass m raised from surface of the earth to a height equal to radius R of the earth is - [M = mass of earth]
View SolutionIf the acceleration due to gravity on the surface of the earth is 9.8m/s2, what will be the acceleration due to gravity on the surface of a planet whose mass and radius both are two times the corresponding quantities for the earth ?
View SolutionWhat is the value of acceleration due to gravity at a height equal to helf the radius of earth, from surface of earth ? [take g=10m/s2 on earth's surface]
View SolutionWhat is the value of acceleration due to gravity at a height equal to half the radius of earth, from surface of earth ? [take g=10m/s2 on earth's surface]
View Solution
