A satellite of mass m is moving in a circular orbit of radius r=(Re+h) around earth of radius Re and mass Me. And density of earth ρ. Match the following
 Solution in Telugu
Solution in Telugu
A-5,B-2,C-4,D-3,E-1
A-4,B-1,C-3,D-2,E-5
A-3,B-2,C-1,D-5,E-4
A-4,B-3,C-2,D-1,E-5
The correct Answer is:A
Step by step video, text & image solution for A satellite of mass m is moving in a circular orbit of radius r=(R_e+h) around earth of radius R_e and mass M_e. And density of earth rho. Match the following by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - Exercise-II
78 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - Practice Exercise
56 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II) PRACTICE SHEET (ADVANCED)Integer Type Questions
6 Videos
- GAUSS.S LAW BOOK - AAKASH SERIESCHAPTER - GAUSS.S LAW EXERCISE - PROBLEMS (LEVEL - II)
12 Videos
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -3
154 Videos
Similar Questions
A planet revolves round the sun in an elliptical orbit of minor and major axes x and y respectively . Then the time period of revolution is proportional to
View SolutionThe period T and mean distance R of a planet from the sun are related by
View SolutionAssume the planetary orbits to be circular and T be the time period of revolution of the earth around the sun of mass M. If the Jupiter.s period of revolution around the sun is K times that of the earth, the velocity of jupiter in heliocentric reference frame is [2πGMTK1/2]14. The product of x and y is
View SolutionA charge q is placed at the centre of the open end of a cyclindrical vessel. Find the flux of the electric through the surface of the vessel.
View SolutionA satellite takes 1/8 years to move round the earth in its permissible orbit of radius R. The period when it revolves round the earth in an orbit of radius '2R' is
View Solutionद्रव्यमान m का एक उपग्रह पृथ्वी - तल से Re ऊँचाई पर पृथ्वी के परितः घूम रहा है | यदि पृथ्वी - तल का गुरुत्वीय त्वरण g हो तथा पृथ्वी की त्रिज्या Re हो, तो उपग्रह की गतिज ऊर्जा होगा :
View Solutionएक उपग्रह जिसका द्रव्यमान m है पृथ्वी की सतह से तनिक ही ऊपर एक कक्षा में घूम रहा है | सिद्ध कीजिए कि उपग्रह की गतिज ऊर्जा GMem/2Re है, जहाँ Me व Re क्रमशः पृथ्वी का द्रव्यमान व त्रिज्या है |यह भी दिखाइए कि उपग्रह का आवर्तकाल है √3π/Gρ, जहाँ ρ पृथ्वी का घनत्व है |
View Solutionएक पिण्ड पृथ्वी (त्रिज्या Re , द्रव्यमान Me ) के केन्द्र से r(>Re) दुरी पर स्थित बिन्दु से पृथ्वी की ओर चलना प्रारम्भ करता है | जब यह पृथ्वी के तल पर पहुँचता है, तो इसका वेग होगा :
View SolutionA satellite of mass m is in circular orbit of radius 3R_E about earth (mass of earth M_E , radius of earth R_E ). How much additional energy is required to transfer the satellite to an orbit of radius 9R_E ?
View Solutionएक उपग्रह पृथ्वी के चारों ओर 6RE अपसौर एवं 2RE उपसौर के साथ दीर्घ वृत्ताकार कक्षा में है, जहाँ RE पृथ्वी की त्रिज्या है। कक्षा (Orbit) की अन्त:केन्द्रीयता (Eccentricity) है-
View Solutionस्तंभ-I से स्तंभ-II का मिलान करें।
वृत्तीय कक्षा में उपग्रह के लिए,
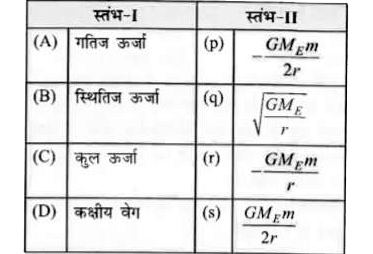
(जहाँ ME पृथ्वी का द्रव्यमान है, m उपग्रह का द्रव्यमान है तथा r कक्षा की त्रिज्या है)
View Solutionm द्रव्यमान का एक उपग्रह पृथ्वी के परित: 2RE त्रिज्या की वृत्तीय कक्षा में है। इसे 4RE त्रिज्या की वृत्तीय कक्षा में स्थानान्तरित करने के लिए आवश्यक ऊर्जा है-
(जहाँ ME एवं RE क्रमश: पृथ्वी का द्रव्यमान एवं त्रिज्या है।)
View Solutionm द्रव्यमान का एक उपग्रह पृथ्वी के परित: 2RE त्रिज्या की वृत्तीय कक्षा में है। इसे 4RE त्रिज्या की वृत्तीय कक्षा में स्थानान्तरित करने के लिए आवश्यक ऊर्जा है-
(जहाँ ME एवं RE क्रमश: पृथ्वी का द्रव्यमान एवं त्रिज्या है।)
स्थितिज ऊर्जा में परिवर्तन है-
View Solutionm द्रव्यमान का क्षुद्रग्रह (Asteroid) पृथ्वी पर आ रहा है, शुरूआत में, 10 RE दूरी तय करने में चाल vi है। यह vf की चाल से पृथ्वी पर आघात करता है। (RE और ME क्रमशः पृथ्वी की त्रिज्या और द्रव्यमान है), तो
View SolutionA satellite is in an elliptical orbit around the earth with aphelion of 6R_E and perihelion of 3R_E , where R_E is the radius of the earth. The eccentricity of the orbit is
View Solution
