A coin is sliding down on a smooth hemi-spherical surface of radius R. The height from the bottom, where it looses contact with the surface is:
R/3
(2R)/3
(3R)/4
(4R)/5
The correct Answer is:B
Topper's Solved these Questions
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - WORK POWER ENERGY (SCALAR OR DOT PRODUCT) (COLLISIONS)
26 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (CENTRE OF MASS)
36 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - WORK POWER ENERGY (SCALAR OR DOT PRODUCT) (POWER)
20 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)
1 Videos
Similar Questions
A small block slides down from the top of hemisphere of radius R = 3 m as shown in the figure. The height 'h' at which the block will lose contact with the surface of the sphere is __________ m.
(Assume there is no friction between the block and the hemisphere)
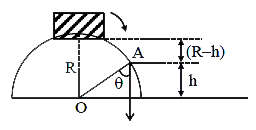
View SolutionA solid sphere of radius R is resting on a smooth horizontal surface. A constant force F is applied at a height h from the bottom. Choose the correct alternative.

View Solution
Knowledge Check
A mass m slips along the wall of a semispherical surface of radius R . The velocity at the bottom of the surface is
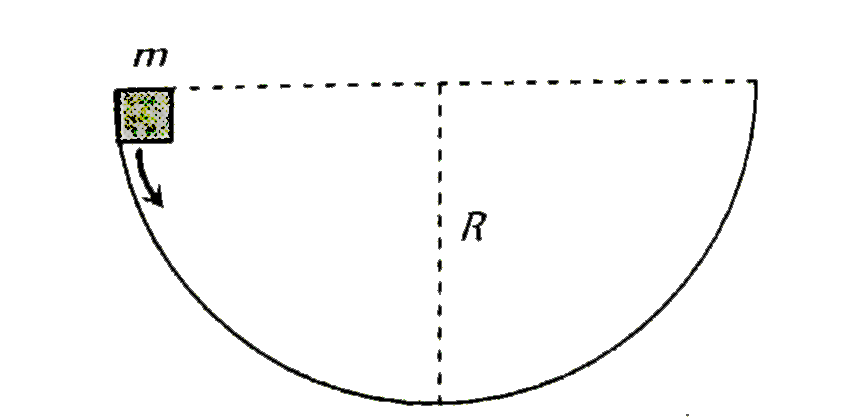 A√RgB√2RgC√λRgD√λRg
A√RgB√2RgC√λRgD√λRgA solid sphere of radius R is resting on a smooth horizontal surface. A constant force F is applied at a height h from the bottom. Vhoose the correct alternative.
 ASphere will always slide whatever be the value of hBSphere will roll without sliding when h≥104RCSphere will roll without sliding if h=1.4RDNone of the above
ASphere will always slide whatever be the value of hBSphere will roll without sliding when h≥104RCSphere will roll without sliding if h=1.4RDNone of the aboveA small body of mass m slides without friction from the top of a hemisphere of radius r. At what height will the body be detached from the surface of hemisphere?
 A32rB23rC12gt2Dv22g
A32rB23rC12gt2Dv22g
At what height (in metres) from the ground would a body sliding over a curved surface of a semi-circular cylinder of radius 6m, kept horizontally on the ground, lose its contact with the surface ?
View SolutionFind total surface area of a solid hemi-sphere of radius 7cm.
View SolutionA body slides down an inclined surface which ends into a vertical loop of radius R = 40cm.
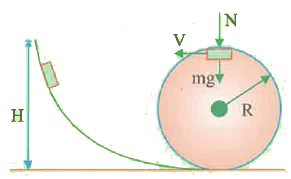
What must be the height H of the inclined surface for the body so that it does not leave contact with the surface even at the uppermost point of the loop? Assume friction to be absent.
View SolutionA particle slides on the surface of a fixed smooth sphere starting from the topmost pont. Find the angle rotated by the radius through the particle, when it leaves contact with the sphere.
View SolutionA block of mass M slides down a rough inclined surface of inclination θ and reaches the bottom at speed at 'v' . However , if it slides down a smooth inclined surface of same length and same inclination , it reaches the bottom with the speed kv. Coefficient of friction between the block and the rough incline is :
View Solution
