A disc rotates freely with rotational kinetic energy E about a normal axis through centre. A ring having the same radius but double the mass of disc is now, gently placed on the disc. The new rotational kinetic energy of the system would be
E/2
(2E)/5
E/5
E/3
The correct Answer is:C
Topper's Solved these Questions
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (ROTATIONAL DYNAMICS)
26 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (ROLLING MOTION)
9 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - SYSTEM OF PARTICLES AND ROTATIONAL MOTION (MOMENT OF INTERTIA)
18 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)
1 Videos
Similar Questions
A horizontal disc rotates freely with angular velocity ω about a vertical axes through its centre. A ring having the same mass and radius as the disc, is now gently placed coaxially on the disc. After some time, the two rotate with a common angular velocity. then.
View SolutionTwo identical discs are positioned on a vertical axis as shown in the figure. The bottom disc is rotating at angular velocity ω0 and has rotational kinetic energy K0.The top disc is initially at rest. It then falls and sticks to the bottom disc. The change in the rotational kinetic energy of the system is

View Solution
Knowledge Check
A horizontal disc rotates freely with angular velocity ω about a vertical axes through its centre. A rig having the same mass and radius as the disc, is now gently placed coaxially on the disc. After some time, the two rotate with a common angular velocity. then.
Ano friction exists between te disc and the ringBthe angular momentum of the system is conservedCthe final common angular velocity is 12ωDall of the aboveA horizontal disc rotates freely about a vertical axis through its centre. A ring, having the same mass and radius as the disc, is now gently placed on the disc. After some time, the two rotate with a common angular velocity, then
Asome friction exists between the disc and the ringBthe angular momentum of the 'disc plus ring' is conservedCthe final common angular velocity is (23)rd of the initial angular velocity of the discD(23)rd of the initial kinetic energy changes to heatA quarter disc of radius R and mass m is rotating about the axis OO' (perpendicular to the plane of the disc) as shown. Rotational kinetic energy of the quarter disc is
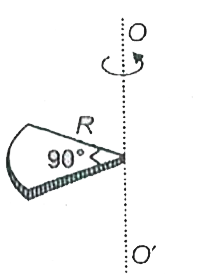 A12mR2ω2B14mR2ω2C18mR2ω2D116mR2ω2
A12mR2ω2B14mR2ω2C18mR2ω2D116mR2ω2
A quarter disc of radius R and mass m is rotating about the axis OO' (perpendicular to the plane of the disc) as shown. Rotational kinetic energy of the quarter disc is

View SolutionA circular disc rolls down an inclined plane . The ratio of rotational kinetic energy to total kinetic energy is
View SolutionWhat is the ratio of the rolling kinetic energy and rotational kinetic energy in the motion of a disc ?
View SolutionA circular disc of mass M1 and radius R, initially moving, With a constant angular speed ω is gently placed coaxially on a stationary circular disc of mass M2 and radius R, as shown in Fig. There is a frictional force between the two discs.
If disc M2 is placed on a smooth surface, then 'determine' the final angular speed of each disc.
b. Determine the work done by friction.
c. Determine the frictional loss in kinetic energy. i.e. △K/Ki
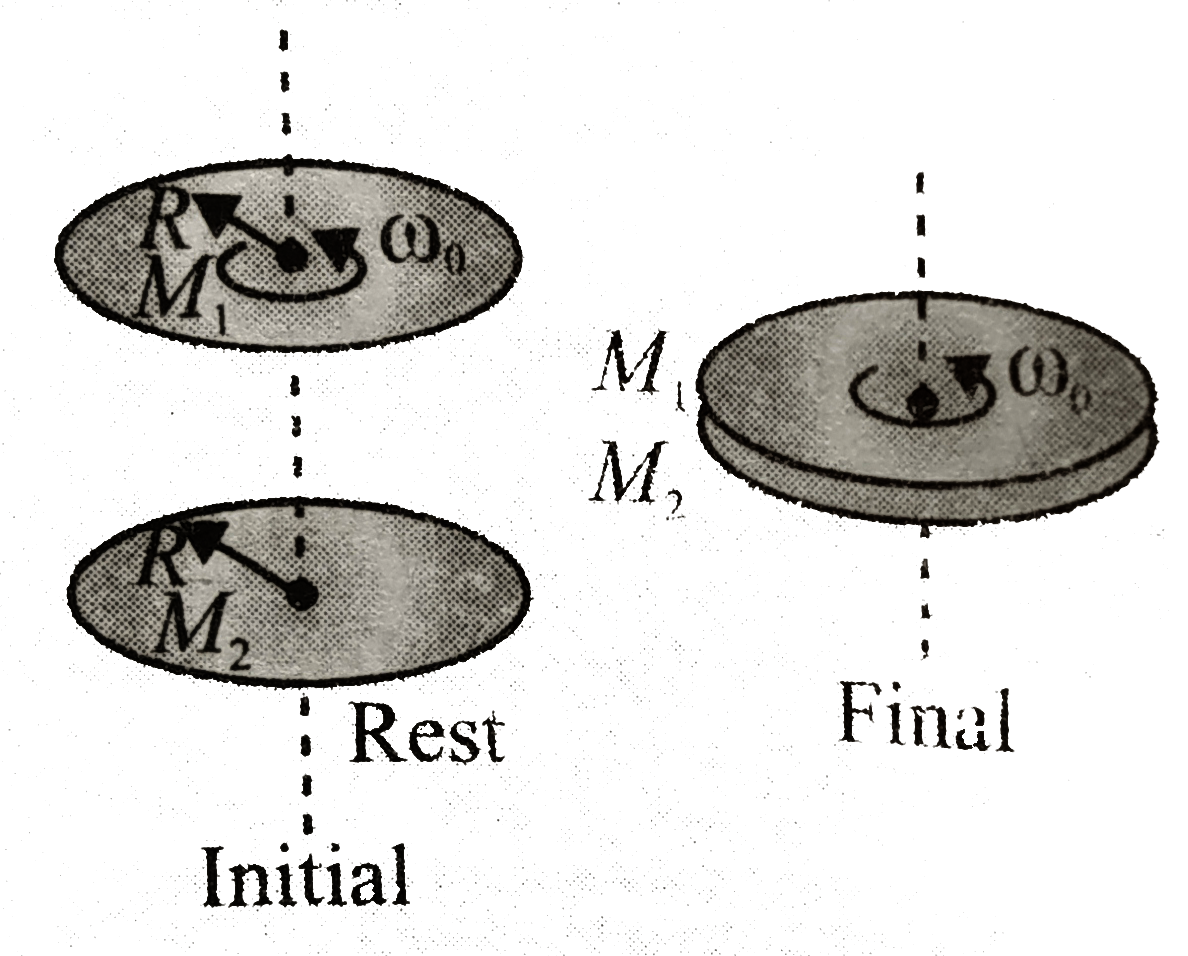
View SolutionA circular disc rolls down an inclined plane . The ratio of rotational kinetic energy to total kinetic energy is
View Solution
