The difference in the value of .g.at pole and at a lattitude is 34Rω2 then latitude angle is
60∘
30∘
45∘
95∘
The correct Answer is:B
Topper's Solved these Questions
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - GRAVITATION (GRAVITATIONAL POTENTIAL ENERGY)
18 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - GRAVITATION (EARTH SATELLITES AND ESCAPE SPEED)
35 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - GRAVITATION (ACCELERATION DUE TO GRAVITY)
10 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)
1 Videos
Similar Questions
Knowledge Check
The difference in the value of g at poles and at a latitude is 34Rω2. The latitude angle is
A60∘B30∘C45∘D95∘The difference in the value of g at poles and at a latitude is 34Rω2. The latitude angle is
A60∘B30∘C45∘D95∘The difference in the value of g at poles and at a sphere of latitude, 45∘ is
ARω2BRω22CRω24DRω23
Which of the following statements related to latitude are true?
1. Rainfall, temperature and vegetation vary with latitude.
2. The difference between the longest day and the shortest day increases with latitude.
3. Indira point is located approximately at 6∘45' N latitude.
Select the correct answer using the code given below.
View SolutionAssuming the earth to be a sphere of radius R, if g30∘ is the value of acceleration due to gravity at latitude of 30∘ and g at the equator, the value of g−g3e∘ is pqω2R, then find (p+q).
View Solution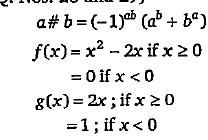
Find the value of f(2#3)#g(3#4) :
View SolutionWeight of a body depends directly upon acceleration due to gravity g. Value of g depends upon many factors. It depends upon the shape of earth, rotation earth etc. Weight of a body at a pole is more then that at a place on equator because g is maximum at poles and minimum on equator. Acceleration due to gravity g varies with latitude λ as per relation given below :
grot=g−Rω2cos2λ where R is radius of earth and ω is angular velocity of earth. A body of mass m weighs Wr in a train at rest. The train then begins to run with a velocity v around the equator from west to east. It observed that weight Wm of the same body in the moving train is different from Wr. Let vebe the velocity of a point on equator with respect to axis of rotation of earth and R be the radius of the earth. Clearly the relative between earth and trainwill affect the weight of the body.
Difference between Weight Wr and the gravitational attraction on the body can be given as
View SolutionR is the radius of the earth and ω is its angular velocity and gp is the value of g at the poles. The effective value of g at the latitude λ=60∘ will be equal to
View Solution
