A system consists of three particles located at the corners of a right triangle as shown in the figure. Find the position vector of centre of mass of the system.
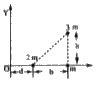
Using the equation
Xc=∑mixiM=2md+m(b+d)+3m(d+b)6m=d+(2/3)b
Yc=∑miyiM=2m(o)+m(o)+3mh6m=h/2
Zc=0, because the particles are in X - Y plane we can express the position of centre of mass from the origin using a position vector as
→rc=Xcˆi+Ycˆj+Zcˆk,→rc=(d+23b)ˆi+h2ˆj
Similar Questions
Knowledge Check
Three particles , each of mass m, are placed at the vertices of a right angled triangle as shown in figure. The position vector of the center of mass of the system is (O is the origin and ˆi,ˆj,ˆk are unit vectors)
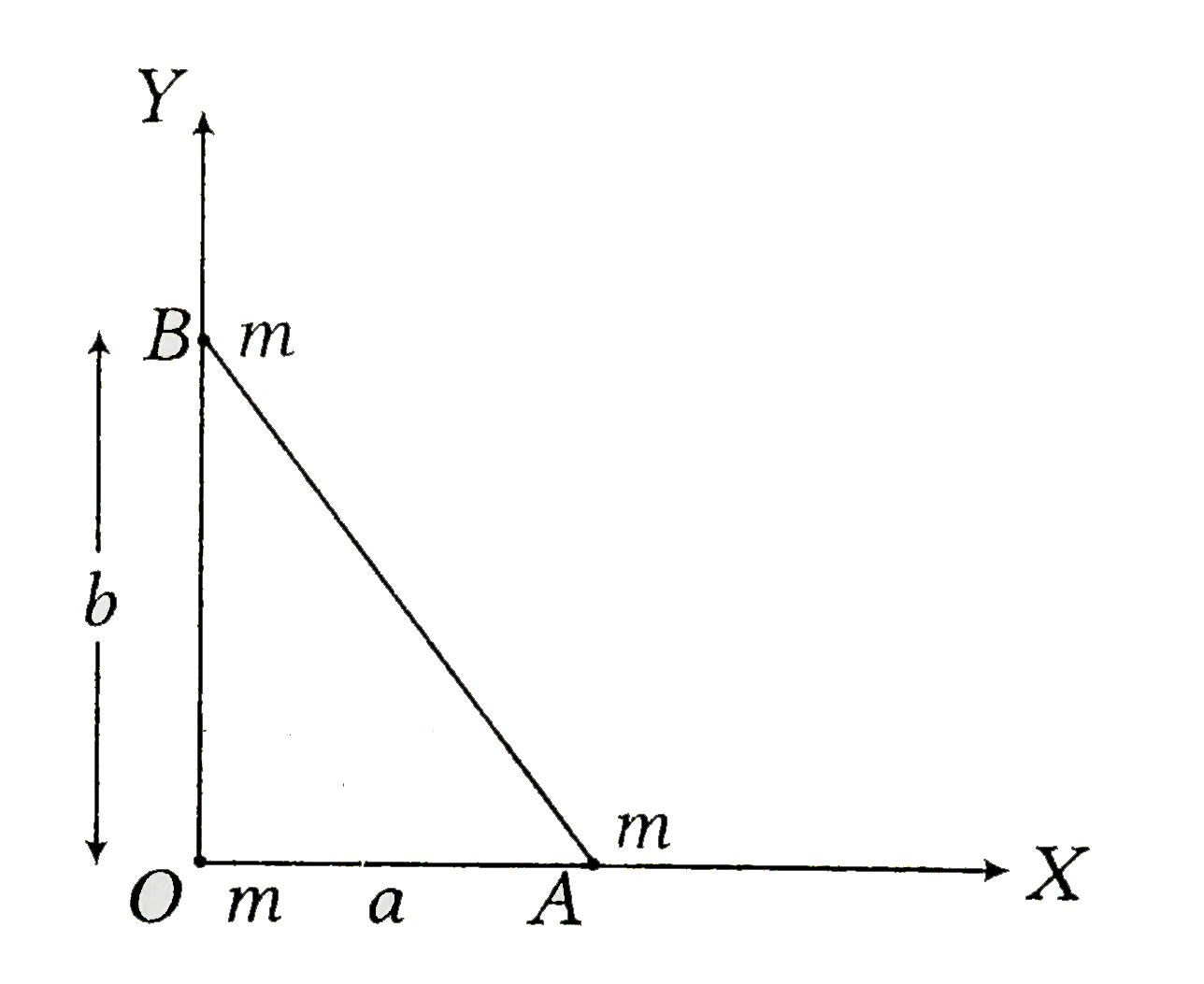 A13(aˆi−bˆj)B23(aˆi−bˆj)C23(aˆi+bˆj)D13(aˆi+bˆj)
A13(aˆi−bˆj)B23(aˆi−bˆj)C23(aˆi+bˆj)D13(aˆi+bˆj)
Obtain an expression for the position vector of centre of mass of a two particle system.
View SolutionObtain an expression for the position vector of centre of mass of a system of n particles.
View SolutionFind centre of mass of a system of three particle kept at the corner equilateral triangle as shown in figure
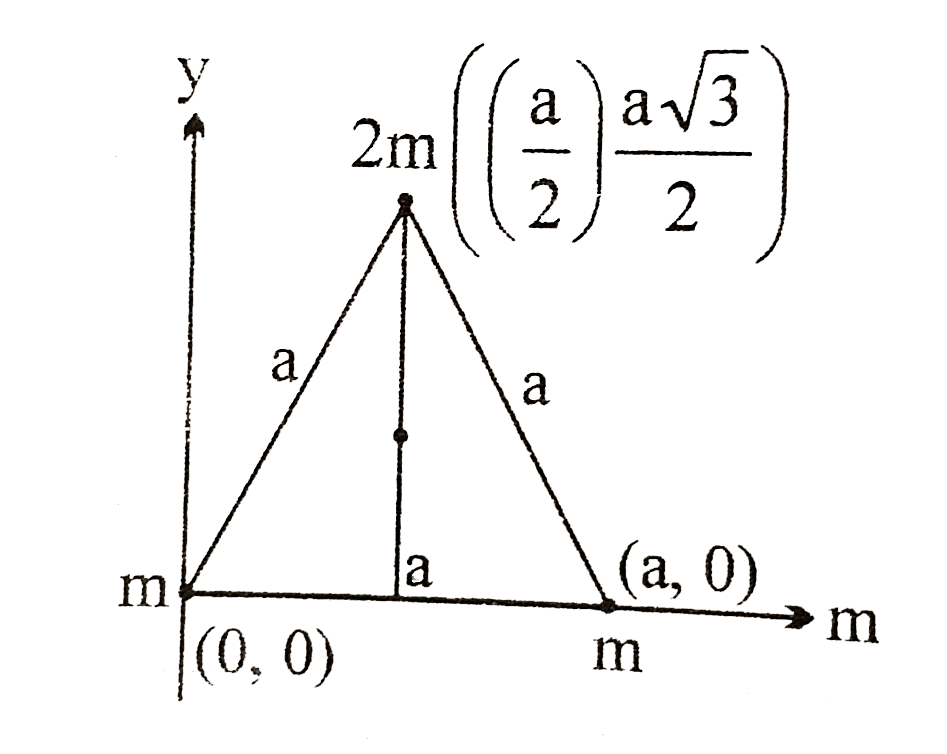
View SolutionThree particles of masses 0.50 kg, 1.0 kg and are placed at the corners of a right angle triangle, as shown in fig. Locate the centre of mass of the system.
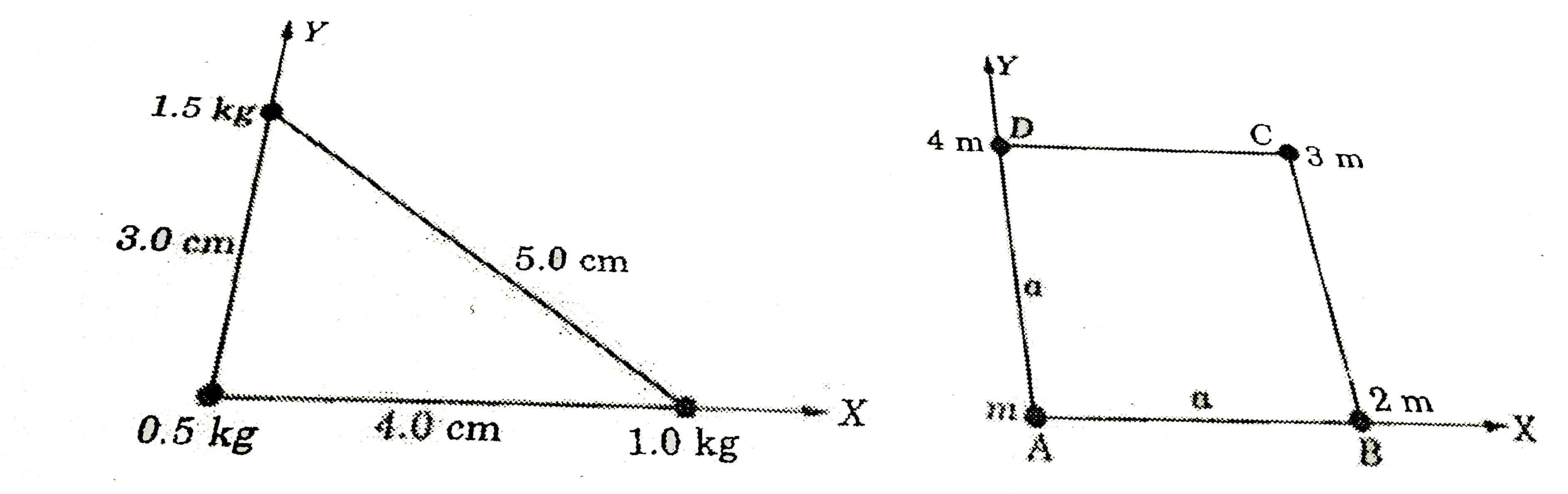
View SolutionThree particles of masses 0.50 kg, 1.0 kg and are placed at the corners of a right angle triangle, as shown in fig. Locate the centre of mass of the system.

View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.

View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.

View Solution

