Two masses m1 and m2 are connected by a spring of force constant k and are placed on a frictionless horizontal surface. Initially the spring is stretched through a distance x0, when the system is released from rest. Find the distance moved by two masses before they again comes to rest.
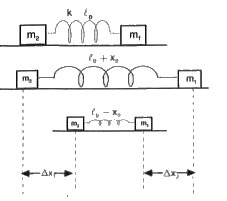
Blocks again come to rest when spring is compressed by x0. Since no external force is acting on the system, so there is no change in the position of c.m. of the system. i.e. Δxcm=0. Let mass m1 displaces by Δx1 and m2 displaces by Δx2, then
We have Δx1+Δx2=2x0...............(i)
and Δxcm=miΔxi+m2Δx2m1+m2
As Δxcm=0∴m1Δx1+m2Δx2m1+m2=0................(ii)
After solving equation (i) & (ii), we get
Δx1=2m2x0m1+m2,Δx2=2m1x0m1+m2
Similar Questions
Two masses m1andm2 re connected by a spring of spring constant k and are placed on as frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
View SolutionTwo masses m1andm2 re connected by a spring of spring constnt k and are placed on as frictionless horizontal surface. Initially the spring is tretched through a distance x0 when the system is released from rest. Find the distance moved by the tow masses before they again come to rest.
View Solution
Knowledge Check
Two masses m1 and m2 connected by a spring of spring constant k rest on a frictionless surface. If the masses are pulled apart and let go, the time period of oscillation is-
AT=2π√1k(m1m2m1+m2)BT=2π√1k(m1+m2m1m2)CT=2π√(m1k)DT=2π√(m2k)Two blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
Athe momentum of each particle remains constant separatelyBthe magnitude of momentums of each body are equal to each otherCthe mechanical energy of system remains constantDboth (C) and (B) are correctTwo blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of osciallation is
A2 cmB1 cmC3 cmD4 cm
Two blocks m1andm2 are connected by a spring of force constant K and are placed on a frictionless horizontal surface. Initially the spring is given extension x0 when the sysetem is released from rest, find the distance moved by two blocks before they again comes to rest.
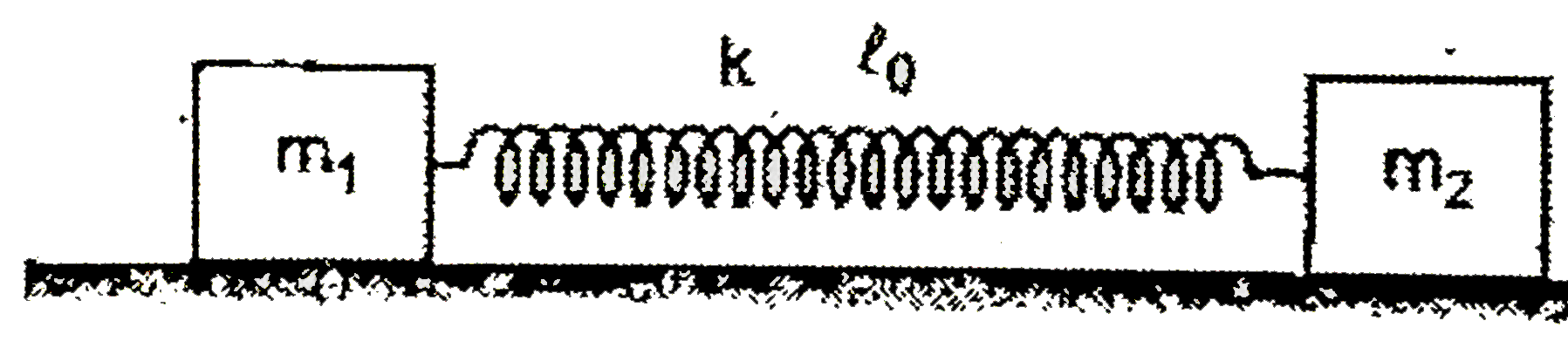
View SolutionTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo blocks A and B of masses m and 2m, respectively , are connected by a massless spring of force constant k and are placed on a smooth horizontal plane. The spring is stretched by an amount x and then released . The relative velocity of the blocks when the spring comes to its natural length is

View Solution
