If the linear density of a rod of length L varies as $λ = A + B x$ , find the position of its centre of mass.

Text Solution

Verified by Experts

Let the x-axis be along the length of the rod and|| origin at one of its ends. As rod is along x-axis, for all points on it y and z co-ordinates are zero.

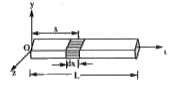
Centre of mass will be on the rod. Now consider an element of rod of length dx at a distance x from the origin, then $d m = λ d x = (A + B x) d x$
$d m = λ d x = (A + B x) d x$ or $X_{C M} = \frac{\frac{A L^{2}}{2} + \frac{B L^{3}}{3}}{A L + \frac{B L^{2}}{2}} = \frac{3 A L + 2 B L^{2}}{3 (2 A + B L)} = \frac{L (3 A + 2 B L)}{3 (2 A + B L)}$

Updated on:21/07/2023

A thin rod of length 6 m is lying along the x-axis with its ends at x=0 and x=6m. Its linear density *mass/length ) varies with x as $k x^{4}$ . Find the position of centre of mass of rod in meters.
A5m
B3m
C2m
D4m
Mass is non-uniformly distributed over the rod of length l, its linear mass density varies linearly with length as $λ = k x^{2}$ . The position of centre of mass (from lighter end) is given by-
A $2 l / 5$
B $3 / l$
C $3 l / 4$
D $2 l / 3$