A roller of mass 300kg rests against a step of height 20 cm. If the radius of the roller is 50 cm find the minimum horizontal force to be applied passing through its center of mass to take the roller on to the step.
Taking the moments of forces about .O.
h=0.2m, R=0.5m , x2=R2−(R−h)2
x=√R2−(R−h)2=0.4m
To climb up the step, moment due to horizontal force ≥ moment due to weight.
F×(R−h)≥mgx
F≥mgxR−h
F≥300×9.8×0.40.3=3920N
Similar Questions

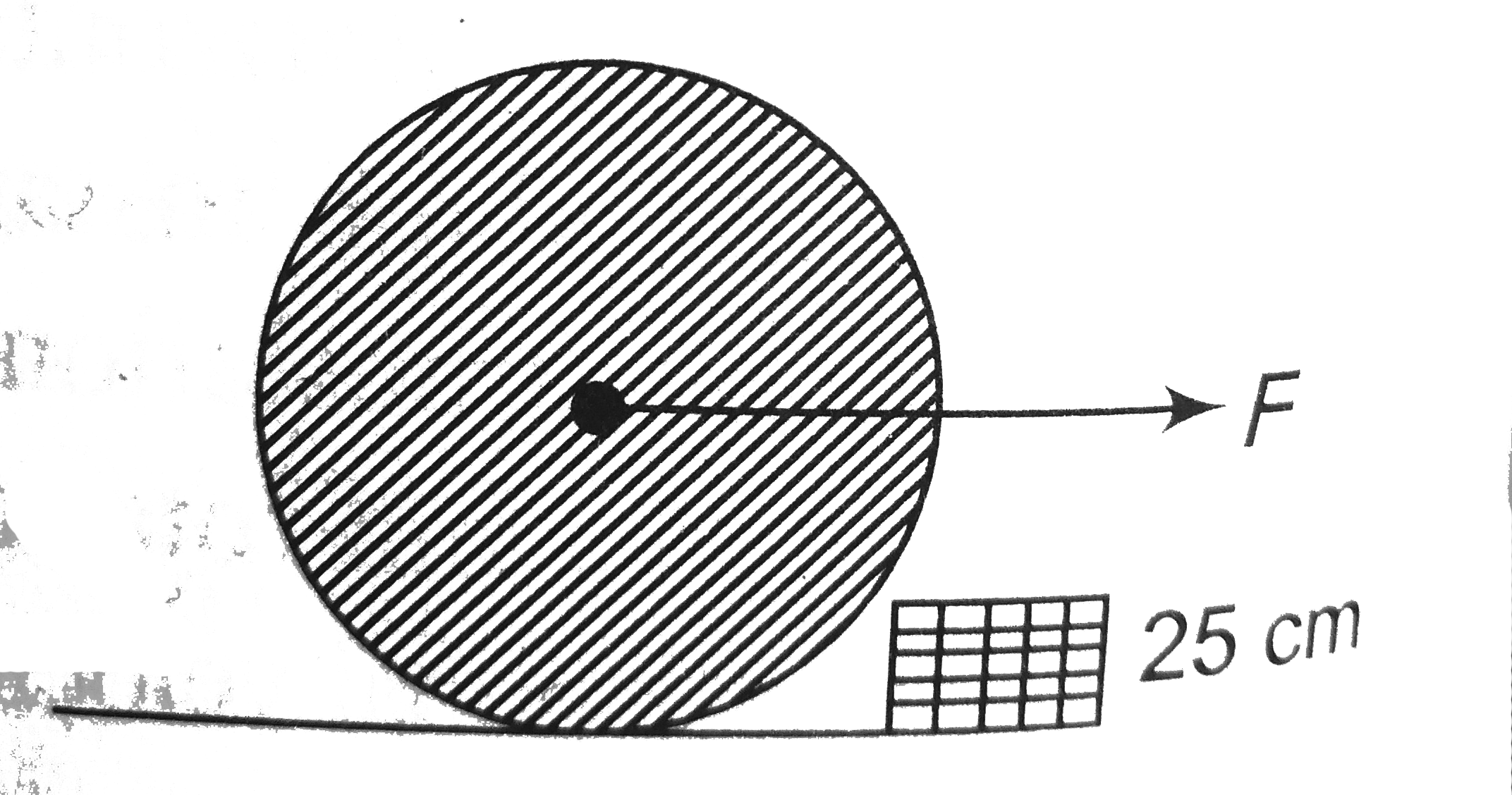
A solid roller having a diameter of 0.82 m is to be raised on to a step of height 32 cm (shown in the figure). If the roller weights 50 kgwt, find the minimum force that can be applied on the roller for the purpose. (Takeg=10ms−2)
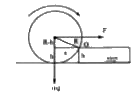
View SolutionThe minimum horizontal force applied to the centre of wheel of radius R and weight w to pull it over a step of height R/2
View Solution
Knowledge Check
A roller of mass 300kg and of radius 50cm lying on horizontal floor is resting against a step of height 20cm. The minimum horizontal force to be applied on the roller passing through its centre to turn the roller on to the step is
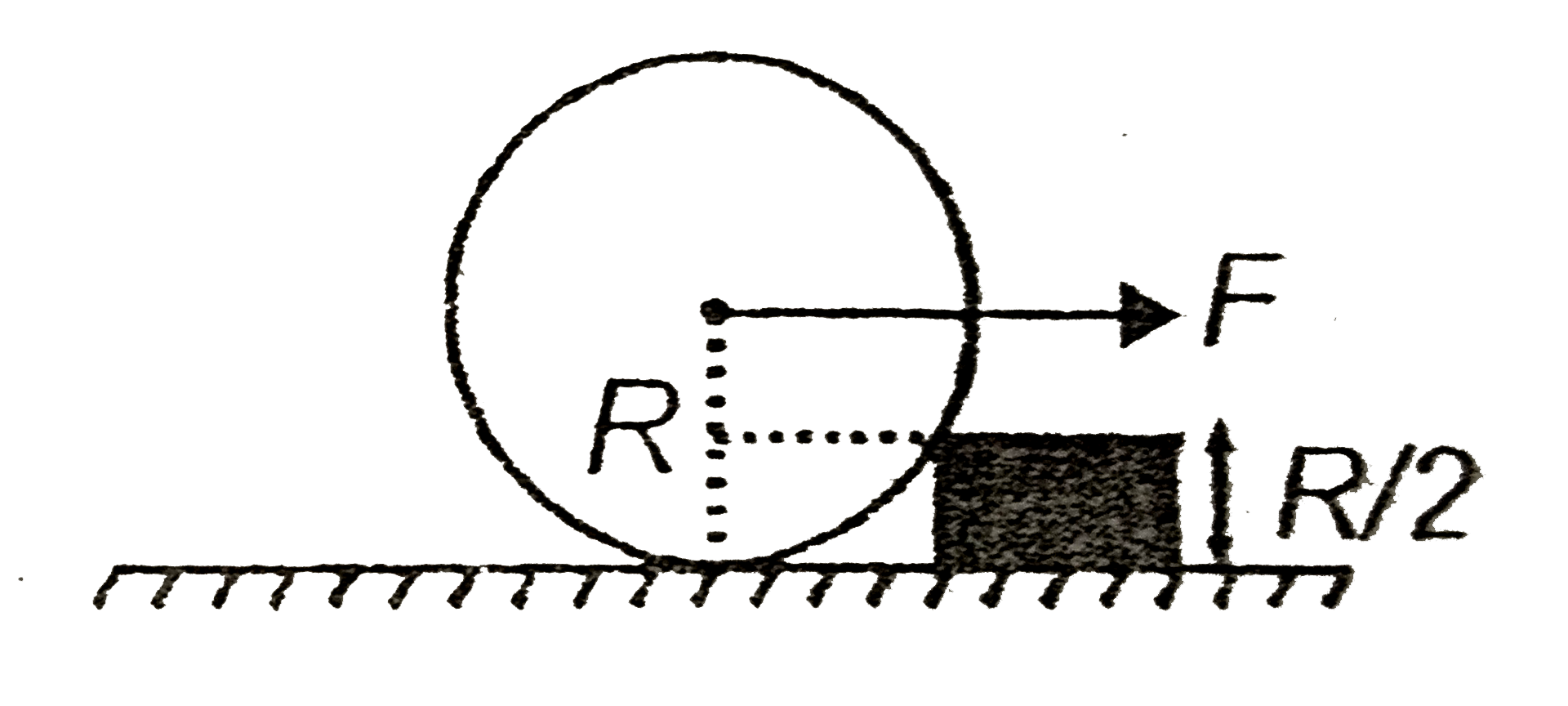
A980NB1960NC2940ND3920NA vertical disc of mass 5kg and radius 50cm rests against a steo of height 25cm as shown in figure. What minimum horizontal force applied perpendicular to the axle will make the disc to climb the step ? Take g=10m/s2.
 .A50 NB50√3NC25NDnone of these
.A50 NB50√3NC25NDnone of theseA heavy wheel of radius 20cm and weight 10kg is to be dragged over a step of height 10cm, by a horizontal force F applied at the centre of the wheel. The minimum value of F is
A20kgwtB1kgwtC10√3kgwtD10√2kgwt
The minimum horizontal force applied to the centre of wheel of radius R and weight w to pull it over a step of height R/2

View SolutionA boy of mass 50kg runs up a staricase of 45 steps in 9s. If the height of each step is 15cm, find his power. Take g=10m/s2
View SolutionA boy of mass 50kg runs up a staricase of 45 steps in 9s. If the height of each step is 15cm, find his power. Take g=10m/s2
View SolutionA boy of mass 50 kg runs up a staircase of 45 steps 9 s. If the height of each step is 15 cm, find his power. Given, g=10 ms−2
View SolutionA small roller of diameter 20 cm has an axle of diameter 10 cm (see figure below on the left). It is on a horizontal floor and a meter scale is positioned horizontally on its axle with one edge of the scale on top of the axel (see figure on the right). The scale is now pushed slowly on the axle so that it moves without slipping on the axle, and the roller without slipping. After the roller has moved 50 cm, the position of the scale will look like (figures are schematic and not drawn to scale)

View Solution
