Molar specific capacity at constant pressure is (RT0m)/(V0) + R

Topper's Solved these Questions

BOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - LECTURE SHEET (EXERCISE - IV (LINKED COMPREHENSION TYPE QUESTIONS))
2videos
THERMODYNAMICS
BOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - LECTURE SHEET (EXERCISE - IV (INTEGER TYPE QUESTIONS))
3videos
THERMODYNAMICS
BOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - LECTURE SHEET (EXERCISE - IV (STRAIGHT OBJECTIVE TYPE QUESTIONS))
3videos
THERMODYNAMICS
BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2videos
THERMAL PROPERTIES OF MATTER
BOOK - AAKASH SERIESCHAPTER - THERMOMETRY EXERCISE - Numerical Exercise (LEVEL- 1)
11videos
THERMOMETRY

Knowledge Check

Question 1 - Select One
A gas is undergoing an adiabatic process. At a certain stage, the volume and absolute temperature of the gas are $V_{0}, T_{0}$ and the magnitude of the slope of the V-T curve is m. molar specific heat of the gas at constant pressure is [Assume the volume of the gas is taken on the y-axis and absolute temperature of the gas taken on x-axis]
A $\frac{m R T_{0}}{V_{0}}$
B $\frac{M R T_{0}}{2 V_{0}}$
C $\frac{(V_{0} + m T_{0}) R}{V_{0}}$
D $\frac{(V_{0} + m T_{0}) R}{2 V_{0}}$
Question 2 - Select One
A gas is undergoing an adiabatic process. At a certain stage A, the values of volume and temperature $(V_{0}, T_{0})$ . From the details given in the graph, find the value of adiabatic constant $γ$

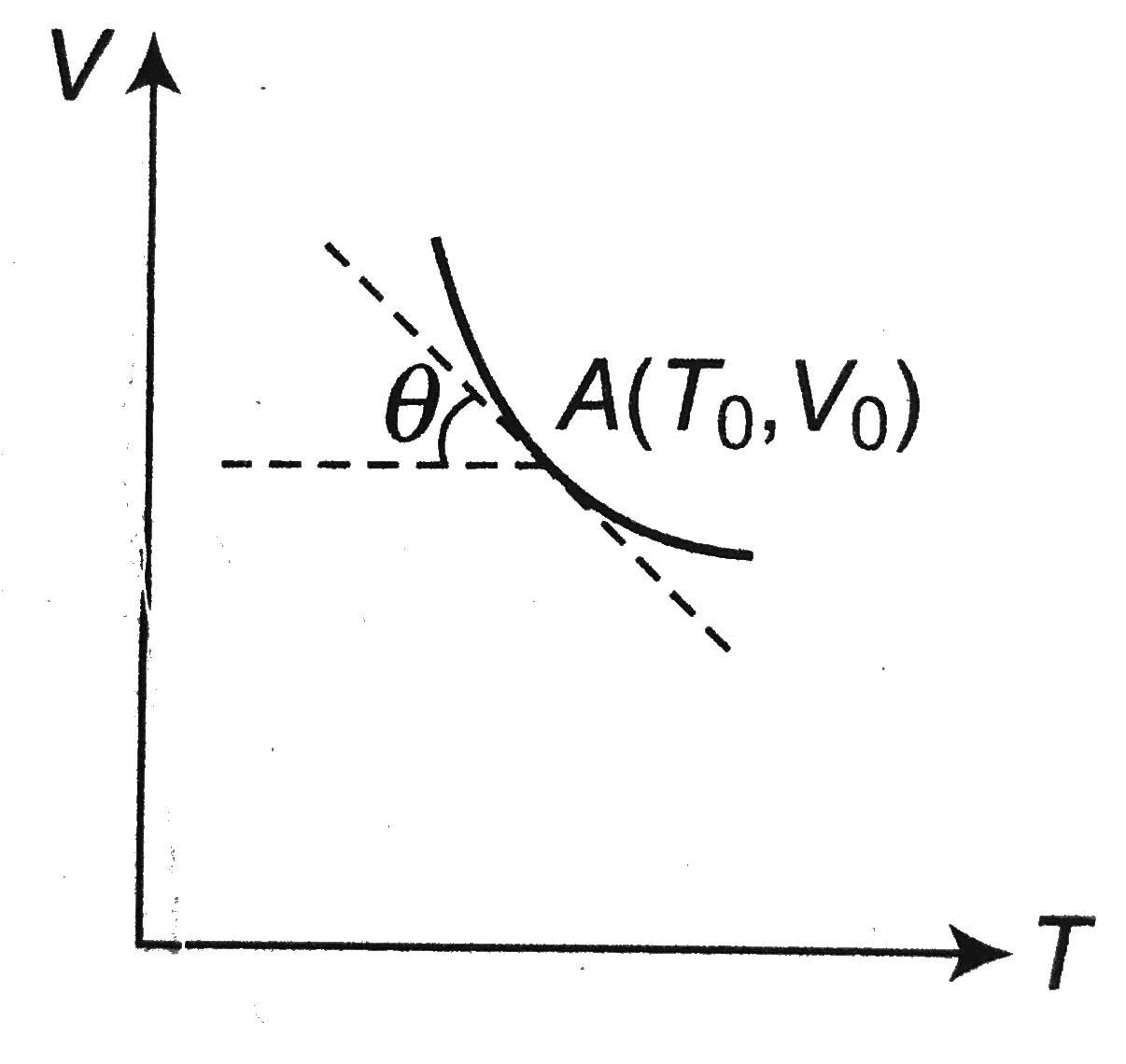A $\frac{V_{0}}{T_{0} tan θ} + 1$
B $\frac{V_{0} tan θ}{T_{0} + 1}$
C $\frac{V_{0} {tan}^{2} θ}{T_{0}} + 1$
D $\frac{V_{0}}{T_{0}} + tan θ$
Question 3 - Select One
One mole of a monatomic ideal gas has an initial pressure, volume, and temperature of $P_{0}, V_{0}$ , and 438 K, respectively. It undergoes an isothermal expansion that triples the volume of the gas. Then, the gas undergoes an isobaric compression back to its original volume. Finally, the gas undergoes an isochoric increase in pressure, so that the final pressure, volume, and temperature are $p_{0} V_{0}$ and 438 K, respectively. Find the total heat for this three-step process, and state whether it is absorbed by or given off by the gas.
A $3640 J$ absorbed
B $- 1820$ J given off
C1570 J , absorbed
D $- 1110 J$ , given off

For a gas undergoing an adiabatic process, at a certain stage its volume and temperature are $V_{0}, T_{0}$ and the magnitude of slope of V - T curve is in

The correct Answer is:A, C, D

Topper's Solved these Questions

Similar Questions

Knowledge Check

A gas is undergoing an adiabatic process. At a certain stage A, the values of volume and temperature $(V_{0}, T_{0})$ . From the details given in the graph, find the value of adiabatic constant $γ$

AAKASH SERIES-THERMODYNAMICS-LECTURE SHEET (EXERCISE - IV (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))

For a gas undergoing an adiabatic process, at a certain stage its volume and temperature are V0,T0 and the magnitude of slope of V - T curve is in

The correct Answer is:A, C, D

Topper's Solved these Questions

Similar Questions

Knowledge Check

A gas is undergoing an adiabatic process. At a certain stage A, the values of volume and temperature (V0,T0). From the details given in the graph, find the value of adiabatic constant γ

AAKASH SERIES-THERMODYNAMICS-LECTURE SHEET (EXERCISE - IV (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))

For a gas undergoing an adiabatic process, at a certain stage its volume and temperature are $V_{0}, T_{0}$ and the magnitude of slope of V - T curve is in

A gas is undergoing an adiabatic process. At a certain stage A, the values of volume and temperature $(V_{0}, T_{0})$ . From the details given in the graph, find the value of adiabatic constant $γ$