A ring consisting of two parts ADB and ACB of same conductivity k carries an amount of heat H. The ADB part is now replaced with another metal keeping the temperatures and constant. The heat carried increases to 2H. What should be the conductivity of the new ADB part? Given :
k
2 k
k
3 k
The correct Answer is:A
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEATEXERCISE - LECTURE SHEET (EXERCISE-I) Thermal Conduction (More than One correct answer Type Questions)4videos
TRANSMISSION OF HEAT
- BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEATEXERCISE - LECTURE SHEET (EXERCISE-I) Thermal Conduction (Linked Comprehension Type Questions) Passage - II3videos
TRANSMISSION OF HEAT
- BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEAT EXERCISE - QUESTION FOR DESCRIPTIVE ANSWER4videos
TRANSMISSION OF HEAT
- BOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTEXERCISE - Practice Exercise45videos
UNITS AND MEASUREMENT
Similar Questions
A ring consisting of two parts ADB and ACB of same conductivity k carries an amount of heat H The ADB part is now replaced with another metal keeping the temperature T1) and T2 constant The heat carried increases to 2H What should be the conductivity of the new ADB Given ACBADB=3
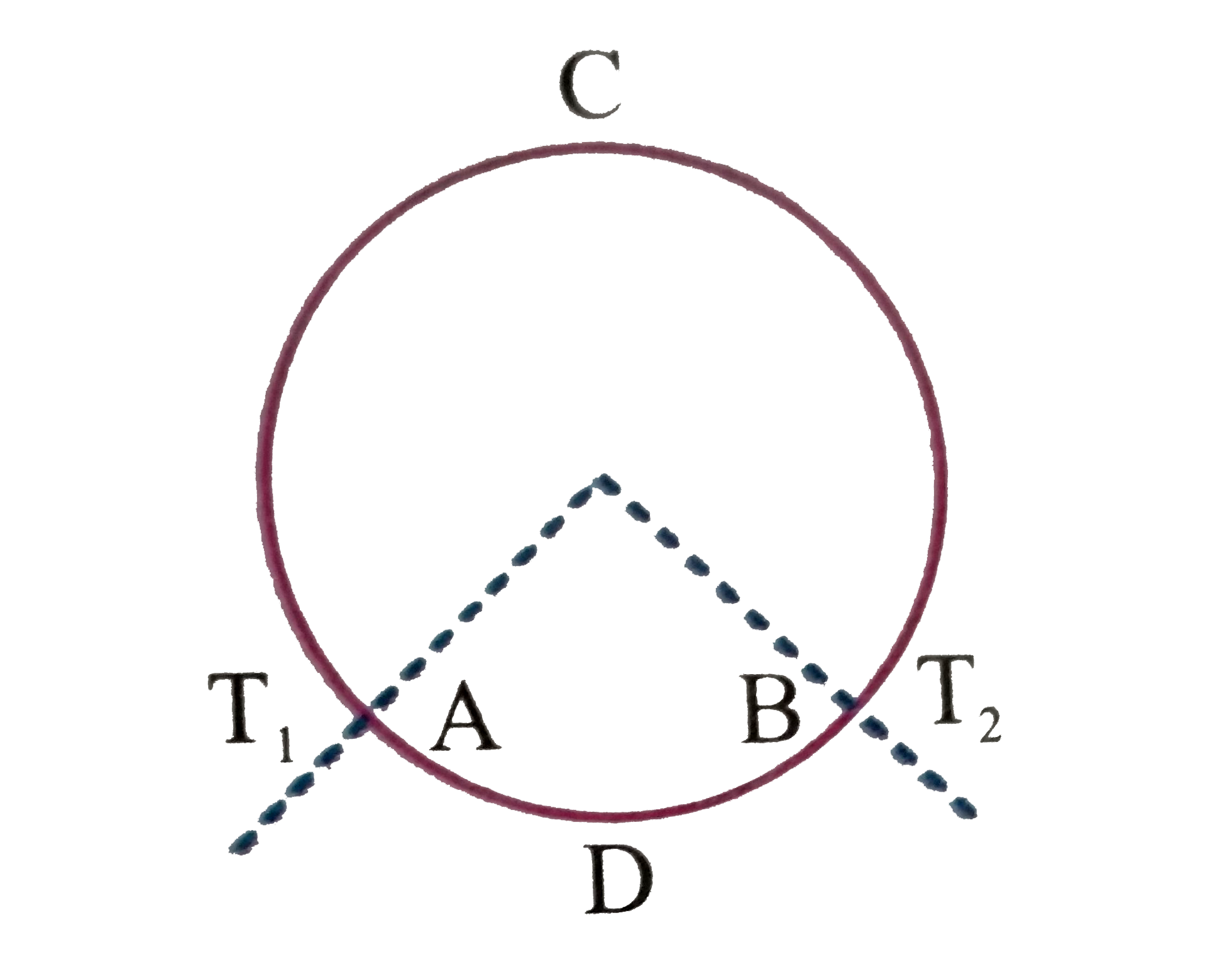 .View Solution
.View SolutionA ring consisting of two parts ADB and ACB of same conductivity k carries an amount of heat H The ADB part is now replaced with another metal keeping the temperature T91) and T2 constant The heat carried increases to 2H What should be the conductivity of the new ADB Given ACBADB=3
 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
A ring consisting of two parts ADB and ACB of same conductivity k carries an amount of heat H The ADB part is now replaced with another metal keeping the temperature T91) and T2 constant The heat carried increases to 2H What should be the conductivity of the new ADB Given ACBADB=3
 .A73KB2KC52KD3K
.A73KB2KC52KD3K - Question 2 - Select One
Consider two rods of same length and different specific heats (S1 and S2), conductivities K1 and K2 and area of cross section (A1 and A2) and both having temperature T1 and T2 at their ends. If the rate of heat loss due to conduction is equal then
AK1A1=K2A2BK2A1=K1A2CK1A1S1=K2A2S2DK2A1S2=K1A2S1 - Question 3 - Select One
A rod of length l and cross sectional area A has a variable conductivity given by K=αT, where α is a positive constant T is temperatures in Kelvin. Two ends of the rod are maintained at temperatures T1 and T2(T1>T2). Heat current flowing through the rod will be
AAαT21−T22lBAαT21+T22lCAαT21+T223lDAαT21−T222l
A ring consisting of two parts ADB and ACB of same conductivity k carries an amount of heat H The ADB part is now replaced with another metal keeping the temperature T91) and T2 constant The heat carried increases to 2H What should be the conductivity of the new ADB Given ACBADB=3
 .View Solution
.View SolutionA ring consisting of two parts ADB and ACB. of same conductivity K carries an amount of heat H. The ADB part is now replaced with another metal keeping the temperature T1 and T2 constant. The heat carried increases to 2H. The conductivity of the new ADB part is x3K. Find the value of x, (Given: ACBADB=3 ) .
'(##CEN_KSR_PHY_JEE_C13_E01_003_Q02##)'View SolutionConsider two rods of same length and different specific heats (S1 and S2), conductivities K1 and K2 and area of cross section (A1 and A2) and both having temperature T1 and T2 at their ends. If the rate of heat loss due to conduction is equal then
View SolutionA rod of length l and cross sectional area A has a variable conductivity given by K=αT, where α is a positive constant T is temperatures in Kelvin. Two ends of the rod are maintained at temperatures T1 and T2(T1>T2). Heat current flowing through the rod will be
View SolutionA rod of length l with thermally insulated lateral surface consists of material whose heat conductivity coefficient varies with temperature as k=a/T, where a is a constant. The ends of the rod are kept at temperatures T1andT2. Find the function T(x), where x is the distance from the end whose temperature is T1.
View Solution

