A 0.60 kg sample of water ans a sample of ice are placed in two compartments A and B that are separated by a conducting wall in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperatures T of the liquid water and the ice are given in graph as functions of time t. Temperatures of the compartments remain homogeneous during the whole heat transfer process.
Given, specific heat of ice = 2100 J/kg-K
Specific heat of water = 4200 J/kg-K
latent heat of fusion of ice = 3.3×10−5 J/kg
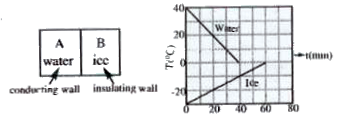
The mass of the ice formed due to conversion from hte water till thermal equilibrium is reached , is equal to
0.12 kg
0.25 kg
0.15 kg
0.40 kg
The correct Answer is:C
Topper's Solved these Questions
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - PRACTICE SHEET (LEVEL - II Matrix Matching Type Questions)
2 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - PRACTICE SHEET (LEVEL - II Integer Type Qustions Type Questions)
4 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - PRACTICE SHEET (LEVEL - II More than One correct Type Questions)
5 Videos
- APPENDICES BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - GRAVITATION (EARTH SATELLITES AND ESCAPE SPEED)
35 Videos
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED))
3 Videos
Similar Questions
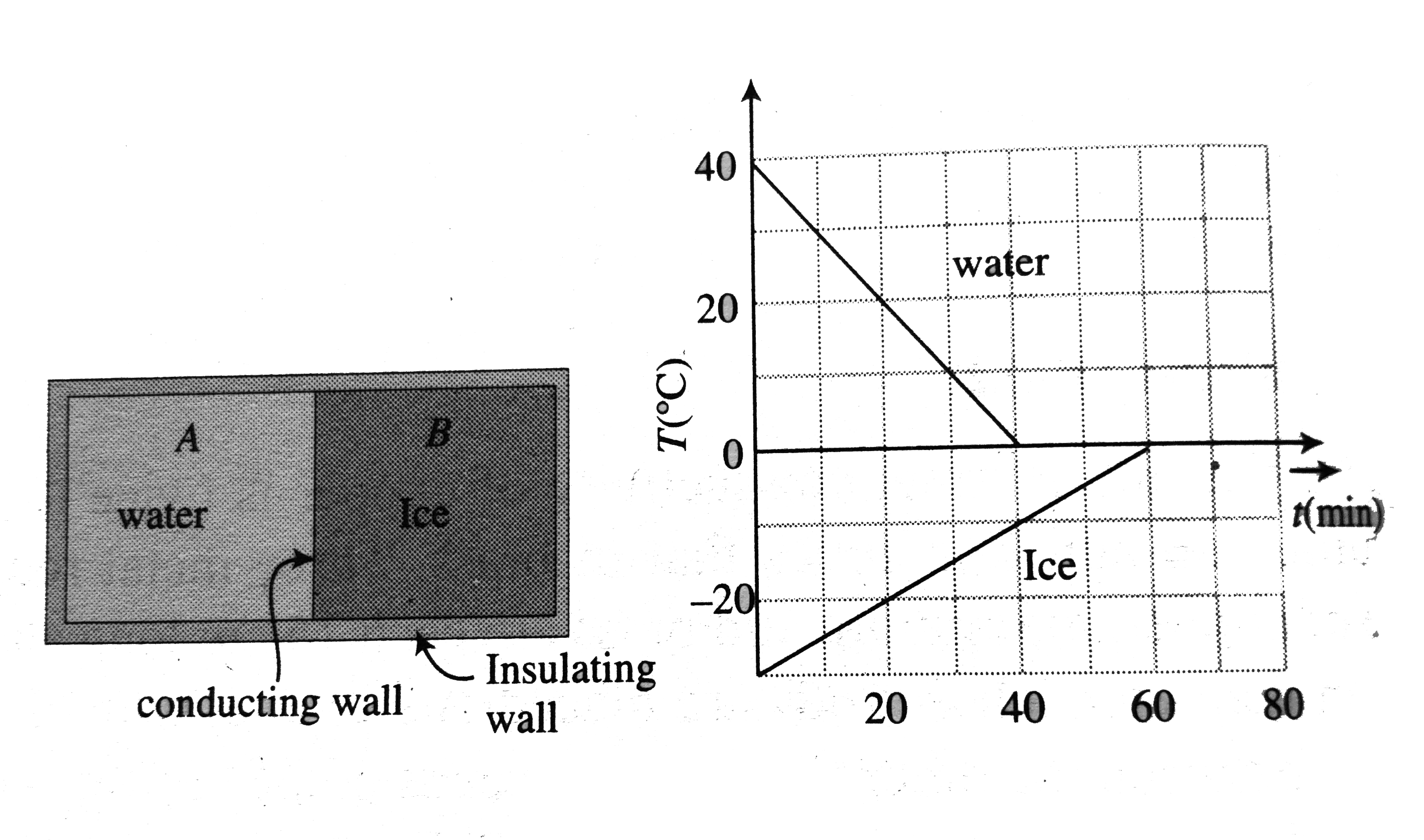
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
View Solution
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
The value of rate P is?
View Solution
Knowledge Check

A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.AThe value of rate P isB42.0 WC36.0 WD21.0 W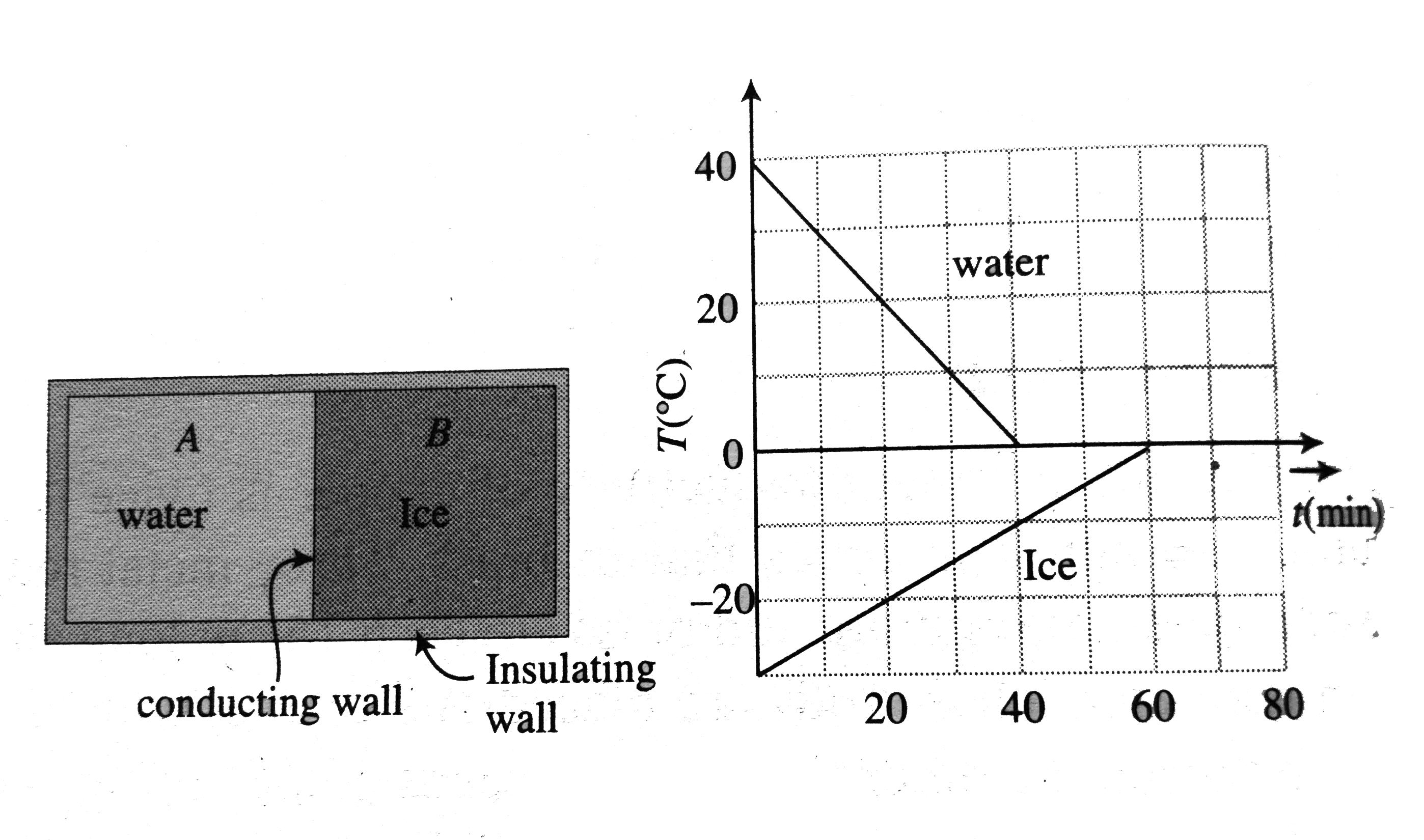
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal toA0.12 kgB0.15 kgC0.25 kgD0.40 kg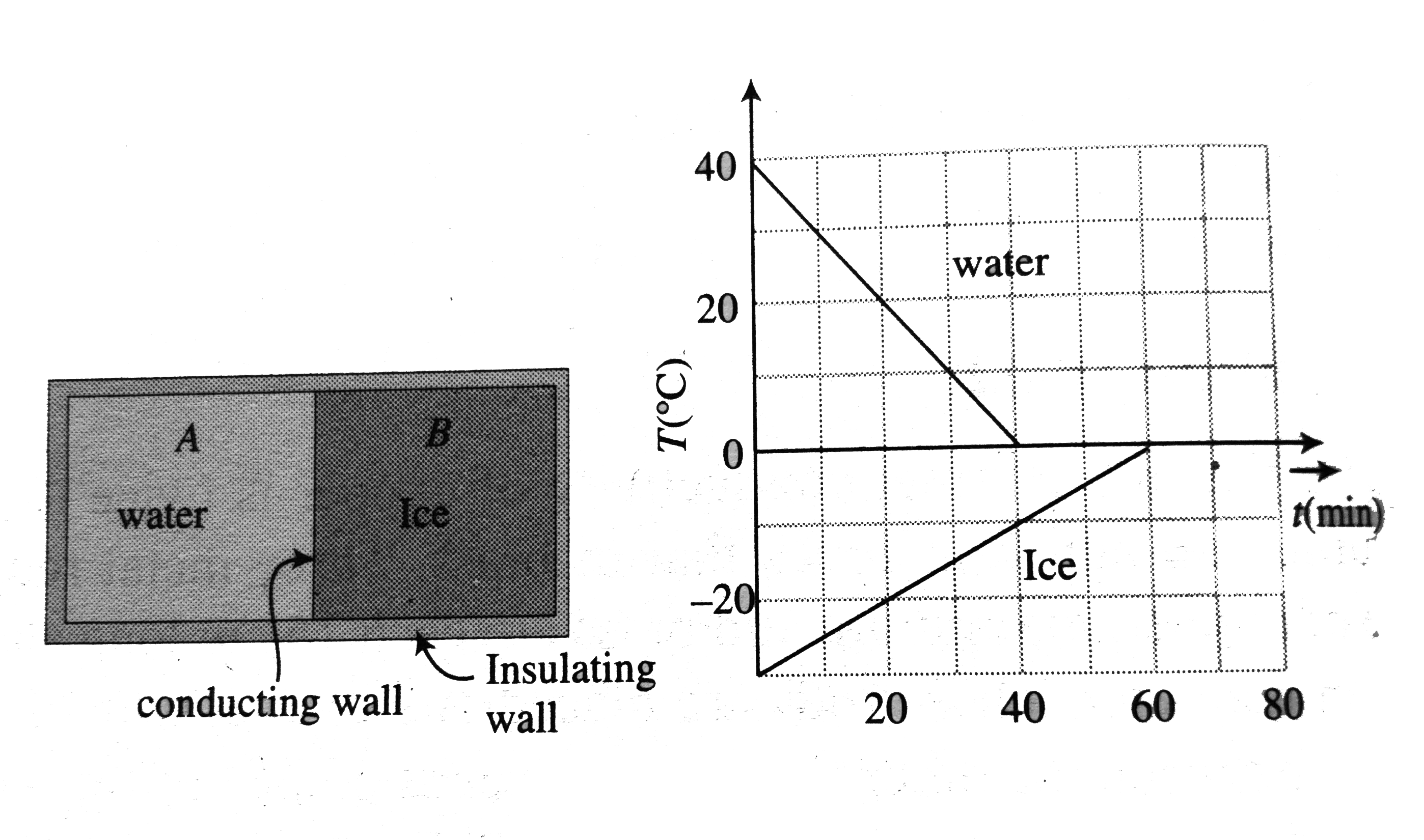
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal toA0.36 kgB1.2 kgC2.4 kgD3.6 kg

A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal to
View Solution
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal to
View Solution
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal to
View Solution
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal to
View Solution(a) Two 40g ice cubes are droped into 200g of water in a thermally insulated container. If the water is initially at 25∘C, and the ice comes directly from a freezer at −15∘C, what is the final temperature at thermal equilibrium? (b) What is the final temperature if only one ice cube is used ?
View Solution
