Keeping the mass of the earth constant, if the radius of the earth decreases by 2%. What would be the change in .g.?

Text Solution
Verified by Experts

We know that the relation between .g. and .G. is g= GMR2
When mass is kept as constant and radius is decreased by 2% thenΔRR×100=2
From distribution of errors in multiplications and divisions Δgg×100=−2ΔRR×100
% change in g=−2×2=−4% -ve sign indicates that when R decreases .g. increases.

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 11PHYSICSGRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The Earth is not a perfect sphere. Due to the flattening of Earth at the poles, the radius of Earth is minimum at the poles and hence the value of g is maximum at the poles. One the other hand, the radius of the Earth is maximum at the equator of the Earth. As the mass and radius of moon are smaller than that of the Earth, so the value of g on moon is 1.63m/s2 . As we go up from the surface of the Earth, the distance from the centre of the Earth increases and hence the value of g decreases. The value of g decreases as we go down inside the Earth and it become zero at the centre of the Earth .
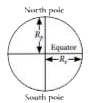
    ocr_image
    If the radius of the Earth were to shrink by 1% and its mass remaining the same, the acceleration due to gravity on the Earth's surface would

    Adecreases
    Bincreases
    Cremain unchanged
    Dwill decrease by 9.8%

  • If both the mass and radius of the earth, each decreases by 50%, the acceleration due to gravity would

    Aremain same
    Bdecrease by 50%
    Cdecrease by 100%
    Dincrease by 100%

  • If both the mass and radius of the earth, each decreases by 50%, the acceleration due to gravity would

    Aremains same
    Bdecreases by 50%
    Cdecreases by 100%
    Dincreases by 100%