An ideal gas is trapped between a mercury column and the closed lower end of a narrow vertical tube of uniform bore. The upper end of the tube is open to the atmosphere. (Atmospheric pressure is 76 cm of mercury). The length of the mercury and the trapped gas columns are 20 cm and 43 cm, respectively. What will be the length of the gas column when the tube is tilted slowly in a vertical plane through an angle of 60∘. Assume the temperature to be constant.
Boyle.s law holds good because the temperature is constant.
So, P1V1=P2V2 or P1l1=P2l2 , since the bore is uniform
P1=76+20=96cm of Hg ,
l1=43cm,P2=76+h=76+20cos60∘=76+10=86cm of Hg
l2=?
∴96×43=86l2
∴l2=48cm of Hg
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - EXPANSION OF GASESEXERCISE - TEST YOUR SELF6videos
EXPANSION OF GASES
- BOOK - AAKASH SERIESCHAPTER - EXPANSION OF GASESEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS18videos
EXPANSION OF GASES
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWER10videos
ELEMENTS OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - EXPANSION OF LIQUIDS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS4videos
EXPANSION OF LIQUIDS
Similar Questions
An ideal gas is trapped between a mercury column and the closed lower end of a narrow vertical tube of uniform bore. The upper end of the tube is open to atmosphere (atmospheric pressure = 76 cm of Hg). The length of mercury and the trapped gas columns are 20 cm and 43 cm respectively. What will be the length of the gas column when the tube is titled slowly at constant temperature in a vertical plane through an angle of 60∘ ?
View SolutionAn ideal gas is trapped between a mercury column and the closed lower end of a narrow vertical tube of uniform bore. The upper end of the tube is open to atmosphere (atmospheric pressure = 76 cm of Hg). The length of mercury and the trapped gas columns are 20 cm and 43 cm respectively. What will be the length of the gas column when the tube is titled slowly at constant temperature in a vertical plane through an angle of 60∘ ?
View Solution
Knowledge Check
- Question 1 - Select One
In the given figure, atmospheric pressure p0=1 atm and mercury column length is 9 cm. Pressure p of the gas enclosed in the tube is
 APressure of 67 cm of HgBPressure of 90 cm of HgCPressure of 78 cm of HgDPressure of 85 cm of Hg
APressure of 67 cm of HgBPressure of 90 cm of HgCPressure of 78 cm of HgDPressure of 85 cm of Hg - Question 2 - Select One
What will be the length of mercury column in a barometer tube when the atmospheric pressure is x cm of mercury and the tube is inclined at an angle ϕ with the vertical direction ?
AxsinϕBxcosϕCxtanϕDx
In given figure, an ideal gas is trapped between a mercury column and the closed end of a uniform vertical tube. The upper end of the tube is open to the atmosphere. Initially the lengths of the mercury column and the trapped air colume are 12cm and 50cm respectively. when the tube is titted solwly in a vertical plane through an angle of 30∘ with horizontal then the new length of air colume is x41m. Find x. Assuming the temperature to remains constant. (Patm=76cmofHg)
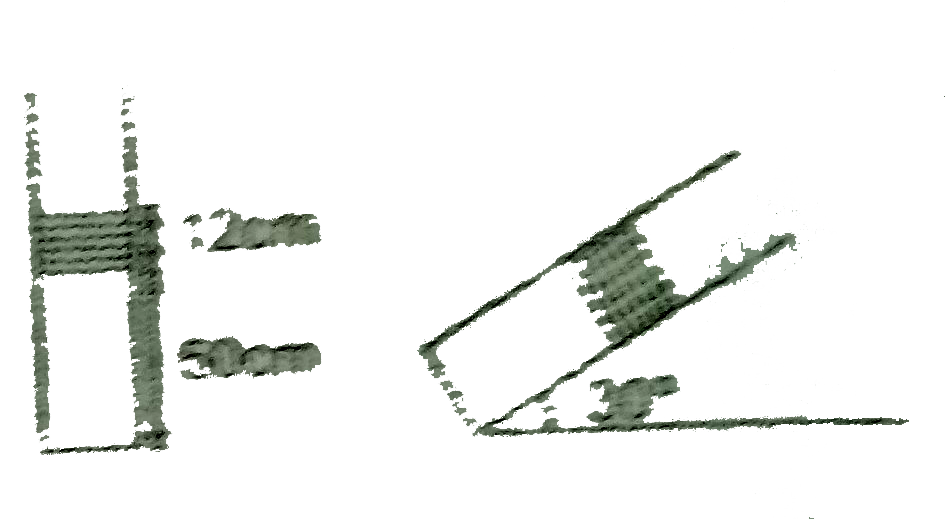 View Solution
View SolutionIn given figure, an ideal gas is trapped between a mercury column and the closed end of a uniform vertical tube. The upper end of the tube is open to the atmosphere. Initially the lengths of the mercury column and the trapped air colume are 12cm and 50cm respectively. when the tube is titted solwly in a vertical plane through an angle of 30∘ with horizontal then the new length of air colume is x41m. Find x. Assuming the temperature to remains constant. (Patm=76cmofHg)
 View Solution
View SolutionCalculate the length of mercury column in a barometer tube which is inclined at an angle of 45∘ with horizontal direction if the atmospheric pressure is 75 cm of mercury.
View SolutionA barometer tube is inclined at an angle of 30∘ with horizontal direction. Calculate length of mercury column in tube if atmospheric pressure is 76 cm of mercury.
View SolutionIn the given figure, atmospheric pressure p0=1 atm and mercury column length is 9 cm. Pressure p of the gas enclosed in the tube is
 View Solution
View SolutionWhat will be the length of mercury column in a barometer tube, when the atmospheric pressure is 76 cm of mercury and the tube is inclined at an angle of 30∘ with the horizontal direction ?
View Solution

