An ideal gas of molecular mass M is located in the uniform gravitational field in which the free-fall acceleration is g. Find the gas pressure as a function of height h, if P is equal P0 at h = 0 and the temperature varies with has T=T0 (1-ah). where a is a positive constant.
We have shown that, dPP=−MgRTdh
Given T=T0(1−ah)
∴dPP=MgRT0(1−ah)dh
Integrating on both sides, we get ∫ppodPP=−MgRT0∫h0dh1−ah
loge(P/P0)=−MgRT0loge(1−ah)(−a) (or) loge(P/P0)=loge(1−ah)n
where n=MgaRT0 (or) PP0=(1−ah)n (or) P=P0(1−ah)n=P0(1−ah)rgaRT
Topper's Solved these Questions
- EXPANSION OF GASESBOOK - AAKASH SERIESCHAPTER - EXPANSION OF GASESEXERCISE - TEST YOUR SELF
6 Videos
- EXPANSION OF GASESBOOK - AAKASH SERIESCHAPTER - EXPANSION OF GASESEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
18 Videos
- ELEMENTS OF VECTORS BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWER
10 Videos
- EXPANSION OF LIQUIDS BOOK - AAKASH SERIESCHAPTER - EXPANSION OF LIQUIDS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
4 Videos
Similar Questions
An ideal gas of molar mass M is located in the uniform gravitational field in which the free-fall acceleration is equal to g. Find the gas pressure as a function of height h. If p=p0 at h=0, and the temperature varies with height as
(a) T=T0(1−ah) ,
(b) T=T0(1+ah),
where a is a positive constant.
View SolutionAn ideal gas of molar mass M is contained in a very tall vertical cylindrical vessel in the uniform gravitational field in which the free-fall acceleration equals to T, find the height at which the centre of gravity of the gas is located.
View Solution
Knowledge Check
Find the minimum attainabel pressure of one mole of an ideal gas. If during its expansion its temprature and volume are related as T=T0+αV2 where T0&α are positive constants
A2R√T0αBR√T0α2CR√T0αDR√T0α4Thermal coefficient of volume expansion at constant pressure for an ideal gas sample of n moles having pressure P0, volume V0, and temperature T0 is
ARP0V0BP0V0RC1T0D1nT0A uniform tube of volume V contains an ideal monatomic gas at a uniform pressure P the temperature of the gas varies linearly along te length of the tube ad T and 2 T are the temperature at the ends.
AThe number of moles of the gas in the tube is PVRTln2BThe number of moles of the gas in the tube is PVRTln4CThe internal energy of the gas in the tube is (3/2)PVDThe internal energy of the gas in the tube is (3/2)nRT.
A tall cylindrical vessel with gaseous nitrogen is located in a uniform gravitational field in which the free-fall acceleration is equal to g. The temperature of the nitrogen varies along the height h so that its density is the same throught the volume. find the temperature gradient dT/dh.
View SolutionAn ideal gas of molar mass M is contained in a tall vertical cylindrical vessel whose base area is S and height h. The temperatuer of the gas is T, its pressure on the bottom bass is p0. Assuming the temperature and the free-fall acceleration g to be independent of the height, find the mass of gas in the vessel.
View SolutionA monatomic ideal gas is contained in a rigid container of volume V with walls of total inner surface area A, thickness x and thermal conductivity K. The gas is at an initial temperature t0 and pressure P0 . Find the pressure of the gas as a function of time if the temperature of the surrounding air is Ts . All temperature are in absolute scale.
View SolutionA uniform tube of volume V contains an ideal monatomic gas at a uniform pressure P the temperature of the gas varies linearly along te length of the tube ad T and 2 T are the temperature at the ends.
View SolutionA resistance coil of resistance r connected to an external battery, is placed inside an adiabatic cylinder fitted with a frictionless platon of mass m and same area A. Initially cylinder contains one mole of ideal gas he. A current through the coil such that temperature of gas varies as T=T0+at+bt2, keeping pressure constant with time t. Atosphere pressure above piston is P0. Find
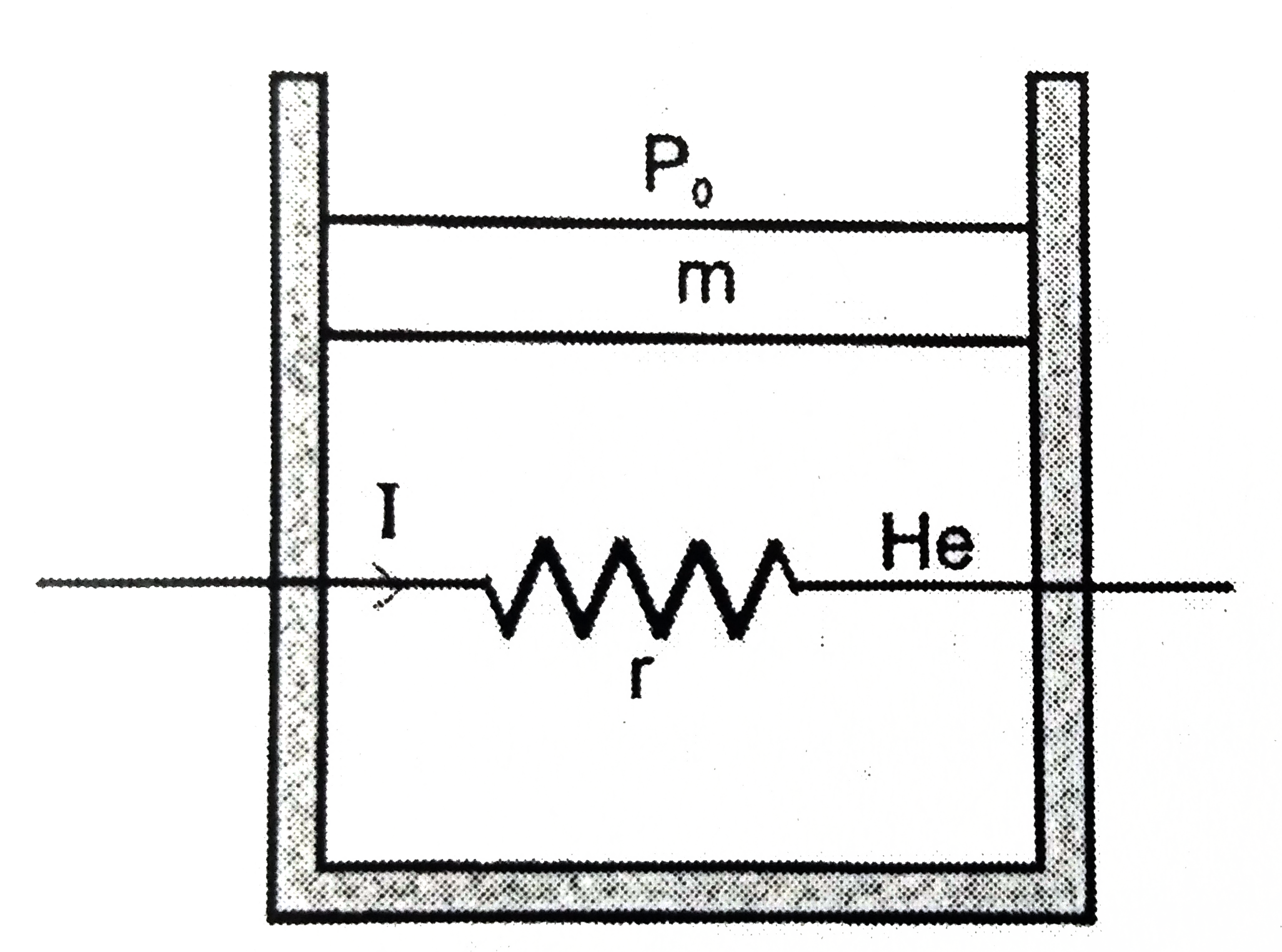
(a) Current l flowing through the coil as function of time and
(b) Speed of piston as function of time.
View Solution
