Question

Three vectors $\overrightarrow{A},\overrightarrow{B},\overrightarrow{C}$ are shown in the figure. Find angle between (i) $\overrightarrow{A}$ and $\overrightarrow{B}$ (ii) $\overrightarrow{B}$ and $\overrightarrow{C}$ (iii) $\overrightarrow{A}$ and $\overrightarrow{C}$.

Explanation

To find the angle between two vectors we connect the tails of the two vectors. We can shift the vectors parallel to themselves such that tails of `vec(A), vec(B)` and `vec(C)` are connected as shown in figure.

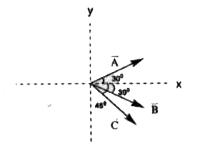
Now we observe that angle between `vec(A)` and `vec(B)` is `60^(@)`, `vec(B)` and `vec(C)` is `15^(@)` nad between `vec(A)` and `vec(C)` is `75^(@)`.