The sum of magnitudes of two forces acting at a point is 16N. If their resultant is normal to the smaller force and has a magnitude of 8N. Then the forces are

Text Solution

Verified by Experts

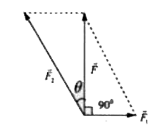
Let $\to F$ be the resultant of two forces ${\to F}_{1}$ and ${\to F}_{2}$ as shown in figure with $F_{2} > F_{1}$ .
$F_{2} sin θ = F_{1}$ ….(i)
$F_{2} cos θ = F = 8$ …..(ii)
Squaring and adding Eqs (i) and (ii), we get
$F_{2}^{2} = F_{1}^{2} + 64$ .....(iii)
Given $F_{1} + F_{2} = 16$ .....(iv)
Solving Eqs. (iii) and (iv), we get
$F_{1} = 6 N$ and $F_{2} = 10 N$

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The sum of two forces at a point is 16N. if their resultant is normal to the smaller force and has a magnitude of 8N, then two forces are
A6N, 10N
B8N, 8N
C4N, 12N
D2N, 14N
Question 2 - Select One
Sum of magitude of two fores is 25 N. The resultant of these forces is normal to the smaller force and has a magnitude of 10 N. Then the two forces are
A $14.5 N, 10.5 N$
B16 N, 9 N
C13 N, 12 N
D20 N , 5 N
Question 3 - Select One
The sum of the magnitudes of two forces acting at a point is 16 N. The resultant of these forces is perpendicular to the smaller force which has a magnitude of 8 N. If the magnitude of smaller force is x, then the value of x is
A2 N
B4 N
C6 N
D7 N

AAKASH SERIES-MOTION IN A PLANE -Practice Exercise

Home
Ask Doubt
Profile