An enemy plane is flying horizontally at an altitude of 2km with a speed of . An army man with an anti-aircraft gun on the ground sights hit enemy plane when it is directly overhead and fires a shell with a muzzle speed of . At what angle with the vertical should the gun be fired so as to hit the plane ?
Let G be the position of the un and E that of the enemy plane flying horizontally with speed
, when the shell is fired with a speed is
Let the shell hit the plane a point P and let t be the time taken for the shell to hit the plane. It is clear that the shell will hit the plane, if the horizontal distance EP travelled by the plane in time t= the distance travelled by the shell in the horizontal direction in the same time,
i.e., or
or
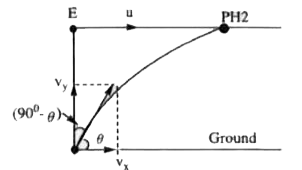
= 0.5 or .
Therefore, angle with the vertical .
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANE EXERCISE - Exercise -I
91 Videos
- MOTION IN A PLANE BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANE EXERCISE - Exercise -II
135 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE - 3
26 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Questions for Descriptive Answers
7 Videos
Similar Questions
An enemy plane is flying horizontally at an altitude of 2km with a speed of 300ms−1.An army man with an anti-aircraft gun on the ground sights enemy plane when it is directly overhead and fires a shell with a muzzle speed of 600ms−1.At what angle with the vertical should the gun be fired so as to hit the plane?
View SolutionAn enemy air plane is flying horizontally at an altitude of 2.7km with a speed of 250ms−1 .An army man on the ground observed it when it is directly over his head.He fired an anti-aircraft gun with a muzzle speed of 500ms−1 ,such that the shell hits the plane.At what angle with the horizontal,gun should be fired?
View Solution
Knowledge Check
A fighter plane flying horizontally at an altitude of 1.5km with speed 720kmh−1 passes directly over head an anticraft gun.
At what angle from the vertical should the gun be fired from the shell with muzzle speed 600ms−1 to hit plane.
At what minimum altitude should the pilot fly the plane to avoid being hit ? ( Take g= 10 ms−2).Asin−1(13) , 16kmBsin−1(23) ,16 kmCcos−1(13) 16mDcos−1(23) ,16mA helicopter is flying horizontally at an altitude of 2km with a speed of 100ms−1 . A packet is dropped from it. The horizontal distance between the point where the packet is dropped and the point where it hits the ground is (g=10ms−2)
A2kmB0.2kmC20kmD4km
A fighter plane flying horizontally at an altitude of 2km with speed of 540 kmph passes directly over head an anti aircraft gun.If the gun can fire a bullet at the muzzle speed of 500ms−1,at what angle with the vertical the gun should fire the bullet so that the bullet hits the plane?
View SolutionA fighter plane flying horizontally at an altitude of 1.5 km with speed 720 km h−1 passes diretly overhead an anti-aircraft gun. At what angle from the vertical should the gun he fired for the shell with muzzle speed 600 m s−1 to hit the plane. (Take g = 10 m s−1)
View SolutionA helicopter is flying horizontally at an altitude of 2km with a speed of 100ms−1 . A packet is dropped from it. The horizontal distance between the point where the packet is dropped and the point where it hits the ground is (g=10ms−2)
View SolutionA fightre plane flying horizontally at an altitude oa 1.5km with speed 720h−1 passes directly over head an anticraft gun. At what angle from the vertical should the gun be fired from the shell with muzzle speed 600ms−1 to hit plane. At what minimum altitude showld the pilot fly the plane to avoid being hit ? ( Take g= 10 ms^(-2)).
View SolutionA fighter plane flying horizontally at an altitude of 1.5km with speed of 720kmh9−10 passes directlu overhead an anticraft gun. At what anle fro the gun with muzzle speed 400ms−1 to hit the plane in shortest time ?
View SolutionA fighter plane is flying horizontally at an altitude of 1.5 km with speed 720kmh−1. At what angle of sight (w.r.t horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target? (Takeg=10ms−2)
View Solution
