Two boys are standing at the ends A and B of a ground where AB = a. They boy at B starts runing in a direction perpendicular to AB with velocity v1. The boy at A starts runing simultaneously with velocity v and catches the other in a time t, where t is
a√v2+v21
av+v1
av−v1
√a2v2−v21
The correct Answer is:D
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANE EXERCISE - Practice Exercise
84 Videos
- MOTION IN A PLANE BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANE EXERCISE - Exercise -I
91 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE - 3
26 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Questions for Descriptive Answers
7 Videos
Similar Questions
Two boys are standing at the ends A and B of a ground where AB = a. The boy at B starts running in a direction perpendicular to AB with velocity v1 . The boy at A starts running simultaneously with velocity v and catches the other in a time t, where t is
View SolutionTwo points P and Q move in a straight line AB. The point P starts from A in the direction AB with velocity u and acceleration f and at the same time Q starts from b in the direction of BA with velocity u1 and acceleration f1. If they pass one another at the middle point of AB and arrive at the other ends of AB with equal velocities, then (u+u1)(f−f1)=8(fu1−f1u).
View Solution
Knowledge Check
Two boys are standing at the ends A and B of a ground, where AB=a. The boy at B starts running in a direction perpendicular to AB with velocity v1. The boy at A starts running simultaneously with velocity v and catches the other boy in a time t, where t is :
Aa√v+v21B√av2+v21Ca(v−v1)Da(v+v1)Two boys are standing at the ends A and B of a ground where AB= a. The boy at B starts running in a direction perpendicular to AB with velocity v. The boy at A starts running simultaneously with velocity v and catches the other in a time t, where t is
Aa√ν2+ν21Baν+ν1Caν−ν1D√a2ν2−ν21A particle moves with an intial velocity v0 and retardation αv, where v is its velocity at any time t.
AThe particle will cover a total distance v0/αBThe particle will come to rest after a time 1/αCThe particle will continue to move for a very long timeDThe velocity of the particle will become v0/2 after a time 1/α
A body starts from rest and acquires a velocity V in a time T.The work done on the body in a time t is proportional to
View SolutionA body A moves with a uniform acceleration a and zero initial velocity. Another body B, starts from the same point moves in the same direction with a constant velocity v. The two bodies meet after a time t. The value of t is
View SolutionA particle moves with an initial velocity v0 and retardation αv, where v is the velocity at any time t.
View SolutionThree particles of equal masses are placed at the corners of an equilateral triangle as shown in the figure. Now particle A starts with a velocity v1 towards line AB, particle B starts with a velocity v2 towards line BC and particle C starts with velocity v3 towards line CA. The displacement of CM of three particle A,B and C after time t will be (given if v1=v2=v3)

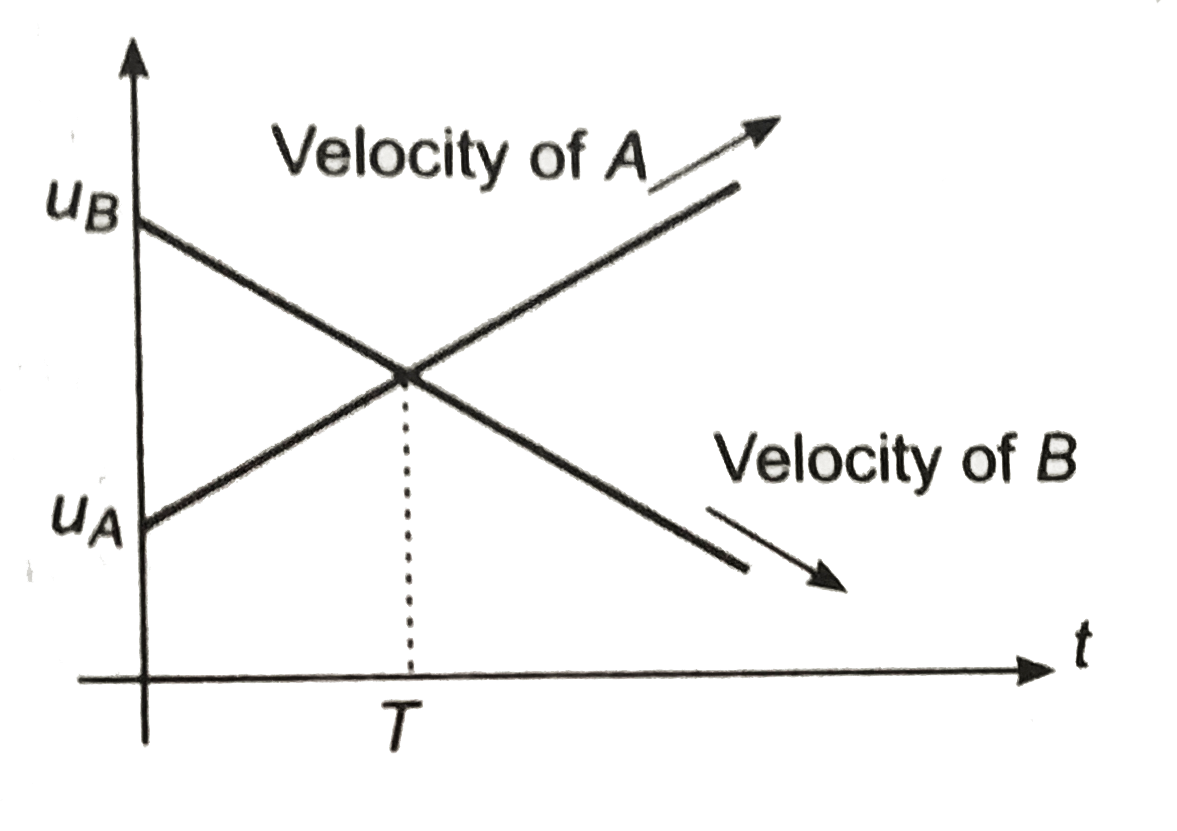
View SolutionA situation is shown in which two objects A and B start their motion from same point in same direction. The graph of their velocities against time is drawn. uAanduB are the initial velocities of A and B respectively. T is the time at which their velocities become equal after start of motion. You cannot use the data of one question while solving another question of the same set. So all the questions are independent of each other.
6. Let vAandvB be the velocities of the particles A and B respectively at the moment A and B meet after start of the motion. If uA=5ms−1anduB=15ms−1, then the magnitude of the difference of velocities vAandvB is
View Solution
