A 0.5 kg ball is suspended to a string of length 1m and is rotated in a vertical plane by holding one end of the string. If it is making 30 rpm, the maximum tension in the string is (π2=10) Solution in Telugu
19.9 N
9.9 N
1.9 N
29.9 N
The correct Answer is:B
Step by step video, text & image solution for A 0.5 kg ball is suspended to a string of length 1m and is rotated in a vertical plane by holding one end of the string. If it is making 30 rpm, the maximum tension in the string is (pi^(2) = 10) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, POWER & ENERGY BOOK - AAKASH SERIESCHAPTER - WORK, POWER & ENERGY EXERCISE - PRACTICE EXERCISE (ELASTIC COLLISIONS)
8 Videos
- WORK, POWER & ENERGY BOOK - AAKASH SERIESCHAPTER - WORK, POWER & ENERGY EXERCISE - PRACTICE EREXCISE (INELASTIC COLLISIONS)
4 Videos
- WORK, POWER & ENERGY BOOK - AAKASH SERIESCHAPTER - WORK, POWER & ENERGY EXERCISE - PRACTICE EXERCISE (POWER)
9 Videos
- WORK POWER ENERGYBOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 3
61 Videos
Similar Questions
A particle of mass m moving with velocity u collides elastically with a particle of mass 3m at rest. After collision the heavier particle moves with velocity.
View SolutionA 2 kg ball moving at 24 ms undergoes inelastic head on collision with a 4 kg ball moving in the opposite direction at 48 ms. If the coefficient of restitution is 2/3, their velocities in ms-after impact are
View SolutionTwo persons A and B each of mass 60 kg are carrying loads 15 kg each. If they reach the top of a building of height 10 m in 20s and 40s respectively, the ratio of their efficiencies is
View SolutionIf →A+→B=→Rand2→A+→B is perpendicular to →B then
View SolutionA string of length L is fixed at one end and carries a mass M at the other end. The string makes 2/π revolution per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is.

View SolutionA string of length 1m is fixed at one end and carries a mass of 1 kg at the other end. The string makes 2//pi revolutions per second around a vertical axis passing through the fixed end. Calculate (i) angle of inclination of the string with the vertical, (ii) the tension in the strong and (iii) the linear velocity of the mass.
View SolutionA string of length L is fixed at one end and carries a mass M at the other end. The string makes 2π rev/s around the vertical axis through the fixed end as shown in figure, then tension in string is
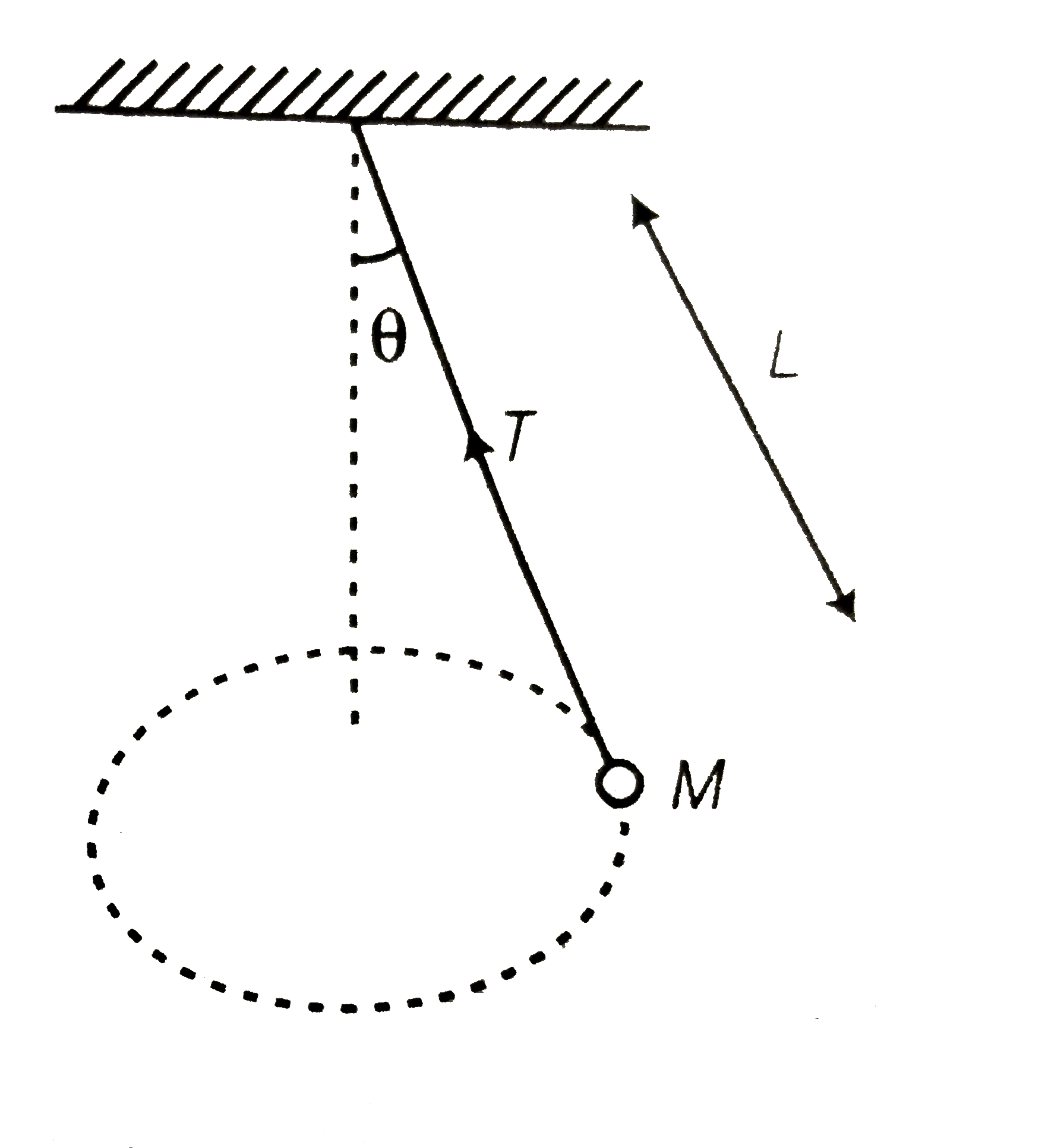
View SolutionA stone is attached to one end of a string and rotated in a vertical circle . If the string breaks at the position of maximum tension , then it will break at
View SolutionA 10 kg steel ball is suspended by two strings as shown. The tensions in the two strings are: (g=9.8 m/s2)

View SolutionA mass of 10 kg is suspended using two strings. One string makes an angle of 60^(@) with the vertical. What should be the angle made by the other string so that the tension in the string will be minimum? Find the tension in each wire.
View SolutionA string will break under a load of 5kg .To the one end of such a 2m long string,a mass of 1kg is attached.The maximum rpm in the horizontal plane,so that the string does not break is ?(g=10m s^(-2) and pi^(2)~~10 )
View SolutionA stone of mas 1 kg is tied to one end of a string of length 0.5 m. It is whirled in a vertical circle. If the maximum tension in the string is 58.8 N, the velocity at the top is
View SolutionA 0.5kg ball is suspended to a string of length 1m and is rotated in a vertical plane by holding one end of the string. If it is making 30r pm, the maximum tension in the string is (π2=10)
View SolutionA stone is attached to one end of a string and rotated in a vertical circle . If the string breaks at the position of maximum tension , then it will break at
View SolutionA string of length L is fixed at one end and carries a mass M at the other end . The string makes 2/π revlutions per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is
View Solution
