Two particles of equal mass move in a circle of radius r under the action of their mutual gravitational attraction . Find the speed of each particle if its mass is m.

Text Solution

Verified by Experts

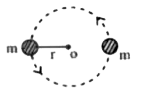
The particle will always remain diametrically opposite , so that the force on each particle will be directed along the radius.
When each particle is describing a circular orbit, the gravitational force on one of the particles must be equal to the necessary centripetal force ,
$\frac{m V^{2}}{r} = \frac{G m m}{{(2 r)}^{2}} i . e V = \sqrt{\frac{G m}{r}}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of each particle is
A $\frac{1}{2 R} \sqrt{(\frac{1}{G m})}$
B $\sqrt{(\frac{G m}{2 R})}$
C $\frac{1}{2} \sqrt{(\frac{G m}{R})}$
D $\sqrt{(\frac{4 G m}{R})}$
Question 2 - Select One
Two particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of earth particle is
A $\frac{1}{3} \sqrt{\frac{G m}{R}}$
B $\frac{1}{2} \sqrt{\frac{G m}{R}}$
C $\frac{1}{2} \sqrt{\frac{R}{G m}}$
D $\sqrt{\frac{G m}{R}}$
Question 3 - Select One
Two particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
A $\frac{1}{2} \sqrt{\frac{G m}{R}}$
B $\sqrt{\frac{4 G M}{R}}$
C $\frac{1}{2 R} \sqrt{\frac{1}{G m}}$
D $\sqrt{\frac{G m}{2 R}}$

AAKASH SERIES-GRAVITATION-ADDITIONAL PRACTICE EXERCISE (LEVEL-II) PRACTICE SHEET (ADVANCED)Integer Type Questions

Home
Ask Doubt
Profile