The radius of a planet is R1anda satellite revolve round of in a circle of radius R2 . The time period of revolution is T. The acceleration due to the gravitation of the planet at its surface is .
Orbital velocity of the satellite V0=√g1R2
where g1=g(R1R2)2
and angular velocity ω=V0R2=√g1R2=
⎷g(R1)2R32
But time period of revolution T=2πω=2π
⎷R32gR21
(or) T2=4π2R32gR21 (or ) g=4π2T2R32R21
Topper's Solved these Questions
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - Exercise-I
124 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - Exercise-II
78 Videos
- GAUSS.S LAW BOOK - AAKASH SERIESCHAPTER - GAUSS.S LAW EXERCISE - PROBLEMS (LEVEL - II)
12 Videos
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -3
154 Videos
Similar Questions
The radius of a planet is R1 and a satellite revolves round it in a circle of radius R2. The time period of revolution is T. find the acceleration due to the gravitation of the plane at its surface.
View SolutionThe radius ofa planet is R1and a satellite revolves round it in a circle of radius R2. The tiemperiod of revolution is T. find the acceleration due to the gravitational of the plane at its surface.
View Solution
Knowledge Check
The radius of a planet is R. A satellite revolves around it in a circle of radius r with angular velocity ω0. The acceleration due to the gravity on planet's surface is
Ar3ω0RBr3ω20R2Cr3ω20RDr3ω20R2The radius of a planet is n times the radius of earth (R). A satellite revolves around it in a circle of radius 4nR with angular velocity ω. The acceleration due to gravity on planet's surface is
ARω2B16 Rω2C32nRω2D64nRω2Two satellites of masses M and 16 M are orbiting a planet in a circular orbitl of radius R. Their time periods of revolution will be in the ratio of
A1:1B1:4C4:1D1:16
The radius of a planet is R. A satellite revolves around it in a circle of radius r with angular velocity ω0. The acceleration due to the gravity on planet's surface is
View Solution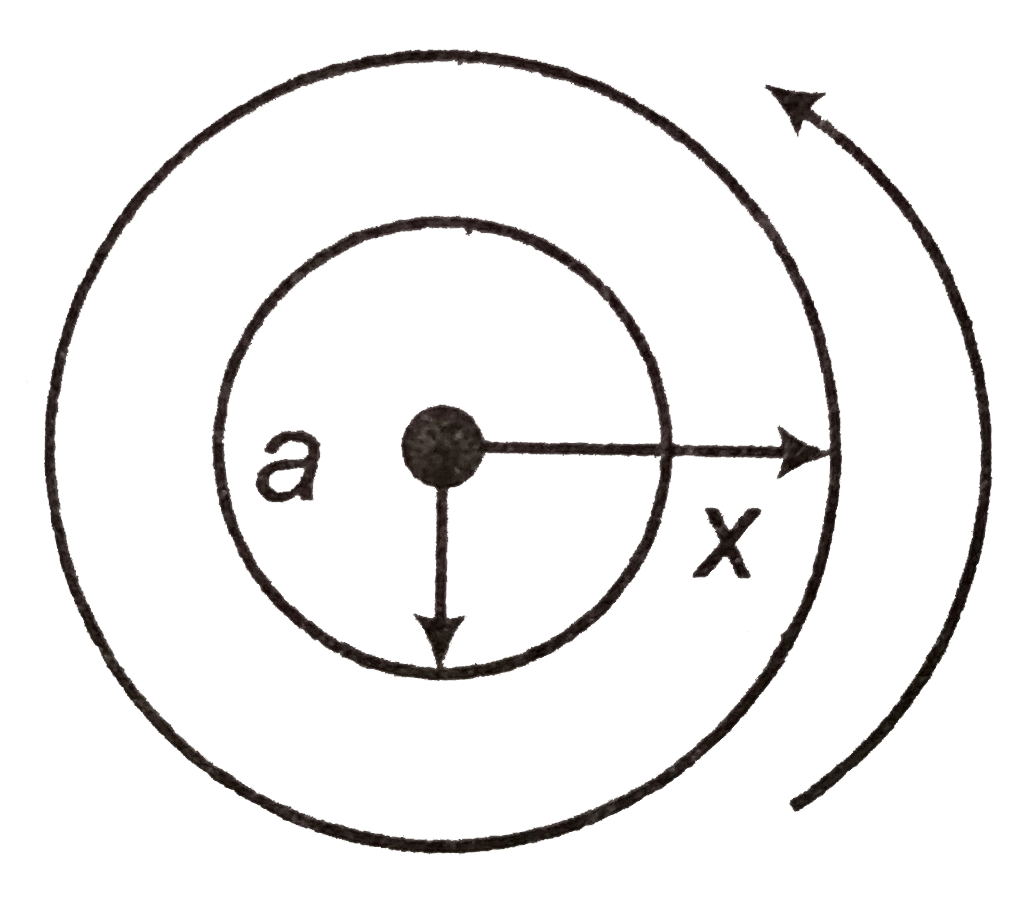
The radius of a planet is a. satelite revolves around it in a circle of radius x with angular velocity ω. The acceleration due to the gravity on planet's surface is
View SolutionTwo satellites of masses M and 16 M are orbiting a planet in a circular orbitl of radius R. Their time periods of revolution will be in the ratio of
View SolutionTwo planets A and B have radius in the ratio 1 : 6. A satellite revolving near the surface of planets have same time period of revolution. The ratio of density of planets A and B is :
View SolutionRadius of a geostationary satellite revolving round the earth is 'r'. Then period of revolution of another satellite revolving in an orbit of radius r/2 is
View Solution
