A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
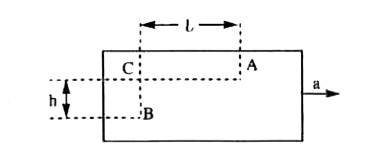
hρg
lρa
hρg−lρa
hρg+lρa
The correct Answer is:D
Similar Questions
A sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be

View SolutionA L Shaped tube containing liquid of density pis accelerated horizontally with acceleration as shown in the figure. The end of tube B is closed while end A is open. If the atmospheric pressure is Po. Then the pressure at B is :
View Solution
Knowledge Check
A sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be
 AhρgBlρgChρg−lρaDhρg−lρa
AhρgBlρgChρg−lρaDhρg−lρa
A vertical communicating tube contains a liquid of density ρ. If it moves with a horizontal acceleration a, pressure at A is equal to :Aρgh2+P0+2Tr2+ρalBρgh2+ρal+P0−2Tr2Cρgh1+P0−2Tr1Dρgh1−P0−2Tr1
A container having a liquid of density ρ is moving downwards with acceleration g2. Find the pressure difference between two vertical points in the liquid separated by h
View SolutionA closed tank filled with water is mounted on a cart. The cart moves with an acceleration 'a' on a plane plane road. What is the difference in pressure between point B and A shown in figure

View SolutionFigure shows a siphon. The liquid shown in water. The pressure difference PB−PA between the points A and B is

View SolutionFigure shows a siphon. The liquid shown in water. The pressure difference PB−PA between the points A and B is

View SolutionA liquid kept in a container has a horizontal acceleration 'a' as shown in figure.
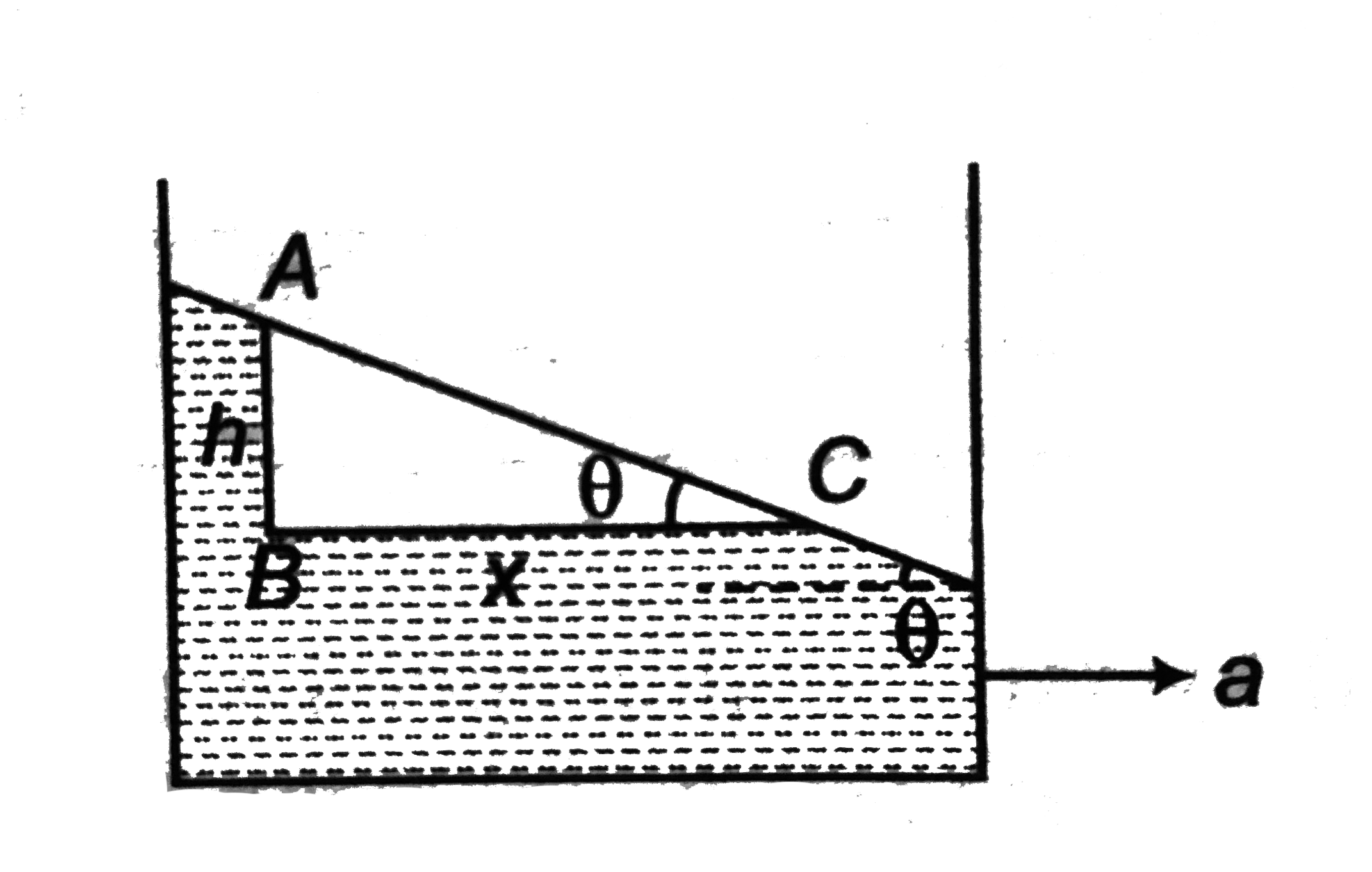
Using the pressure equation along the path ABC find the angle θ.
View SolutionA liquid kept in a container has a horizontal acceleration 'a' as shown in figure.

Using the pressure equation along the path ABC find the angle θ.
View Solution
