Complete the following statements.
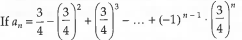and $b_{n} = 1 - a_{n}$ then the smallest natural number $n_{0}$ , such that $b_{n} > a_{n} V n t n > n_{0}$ is

Video Solution

Answer

Step by step video & image solution for Complete the following statements. and b_n=1-a_n then the smallest natural number n_0, such that b_n > a_n Vnt n> n_0 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Some New Pattern ProblemsBOOK - A DAS GUPTACHAPTER - Some New Pattern ProblemsEXERCISE - Exercise
137 Videos
Screening TestsBOOK - A DAS GUPTACHAPTER - Screening TestsEXERCISE - Exercise
38 Videos
Total Conditional Probability and Bayes' TheoremBOOK - A DAS GUPTACHAPTER - Total Conditional Probability and Bayes' TheoremEXERCISE - Exercise
29 Videos

Knowledge Check

For natural number $n, 2^{n} (n - 1)! < n^{n},$ if
A $n < 2$
B $n > 2$
C $n \geq 2$
DNever
For natural number n , $2^{n} (n - 1)! < n^{n}$ , if
A $n < 2$
B $n > 2$
C $n \geq 2$
D $n > 3$
Consider the following two statements :
I. if n is a composite number, then n divides (n – 1)!
II. There are infinitely many natural numbers n such that $n^{3} + 2 n^{2} + n$ divides n!.
Then
AI and II are true
BI and II are false
CI is true and II is false
DI is false and II is true

A DAS GUPTA-Some New Pattern Problems-Exercise

Home
Ask Doubt
Profile

Complete the following statements. and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is

Topper's Solved these Questions

Similar Questions

Knowledge Check

For natural number n,2n(n−1)!<nn, if

For natural number n , 2n(n−1)!<nn , if

Consider the following two statements : I. if n is a composite number, then n divides (n – 1)! II. There are infinitely many natural numbers n such that n3+2n2+n divides n!. Then

A DAS GUPTA-Some New Pattern Problems-Exercise

Complete the following statements.
and $b_{n} = 1 - a_{n}$ then the smallest natural number $n_{0}$ , such that $b_{n} > a_{n} V n t n > n_{0}$ is

For natural number $n, 2^{n} (n - 1)! < n^{n},$ if

For natural number n , $2^{n} (n - 1)! < n^{n}$ , if

Consider the following two statements :
I. if n is a composite number, then n divides (n – 1)!
II. There are infinitely many natural numbers n such that $n^{3} + 2 n^{2} + n$ divides n!.
Then